题目内容
已知圆 C方程为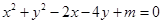 .
.
(1)若圆C与直线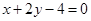 相交于M、N两点,且OM⊥ON(O为坐标原点),求m;
相交于M、N两点,且OM⊥ON(O为坐标原点),求m;
(2)在(1)的条件下,求以MN为直径的圆的方程.
【答案】
(1)m=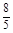 .(2)x2+y2-
.(2)x2+y2-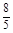 x-
x-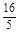 y=0.
y=0.
【解析】(1)设M(x1,y1),N(x2,y2),然后根据OM⊥ON可得x1x2+y1y2=0,
所以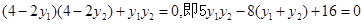 ,然后直线x+2y-4=0与圆方程联立,消去x得关于y的一元二次方程,借助韦达定理代入上式即可得到关于m的方程,求出m的值.
,然后直线x+2y-4=0与圆方程联立,消去x得关于y的一元二次方程,借助韦达定理代入上式即可得到关于m的方程,求出m的值.
(2) 因为以MN为直径的圆的方程为(x-x1)(x-x2)+(y-y1)(y-y2)=0
即x2+y2-(x1+x2)x-(y1+y2)y=0,然后将(1)中x1+x2,y1+y2的值代入即可.
(1)设M(x1,y1),N(x2,y2),
则x1=4-2y1,x2=4-2y2,则x1x2=16-8(y1+y2)+4y1y2
∵OM⊥ON,∴x1x2+y1y2=0 ∴16-8(y1+y2)+5y1y2=0 ①
由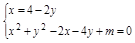 得5y2-16y+m+8=0
得5y2-16y+m+8=0
∴y1+y2=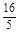 ,y1y2=
,y1y2=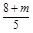 ,代入①得,m=
,代入①得,m=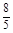 .
.
(2)以MN为直径的圆的方程为
(x-x1)(x-x2)+(y-y1)(y-y2)=0 即x2+y2-(x1+x2)x-(y1+y2)y=0
∴所求圆的方程为x2+y2-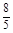 x-
x-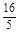 y=0.
y=0.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
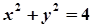
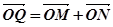 ,求动点Q的轨迹方程。
,求动点Q的轨迹方程。