Question

【题目】已知椭圆C： =1（a＞b＞0）的短轴一个端点到右焦点F的距离为2，且过点 ．
（1）求椭圆C的方程；
（2）设M，N为椭圆C上不同的两点，A，B分别为椭圆C上的左右顶点，直线MN既不平行与坐标轴，也不过椭圆C的右焦点F，若∠AFM=∠BFN，求证：直线MN过定点．

Answer 1

【答案】
（1）

解：由题意可知：短轴一个端点到右焦点F的距离为2，则a=2，

将 代入椭圆方程可得 ，解得：b2=1，

∴椭圆的标准方程：

（2）

证明：由（1）可知：F（ ，0），

设直线MN的方程y=k1x+m，（k≠0），M（x1，y1），N（x2，y2）．

则 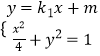，整理得：（1+2k12）x2+8k1mx+4m2﹣4=0，

x1+x2=﹣ ，x1x2= ，

由∠AFM=∠BFN，则kFM+kFN=0， + =0，

（k1x1+m）（x2﹣ ）+（k1x2+m）（x1﹣ ）=0，

整理得：2k1x1x2﹣（m﹣ k1）（x1+x2）﹣2 m=0，

则2k1× ﹣（m﹣ k1）（﹣ ）﹣2 m=0，

解得：m=﹣ k1，

∴直线MN的方程为y=k1（x﹣ ），

则直线MN过定点（ ，0）

【解析】（1）由题意可知：a=2，将点代入椭圆方程，即可求得b的值，即可求得椭圆方程；（2）设直线MN的方程y=k1x+m，代入椭圆方程，由韦达定理，及kFM+kFN=0，即可求得m=﹣ k1 ， 直线MN的方程为y=k1（x﹣ ），则直线MN过定点（ ，0）．