题目内容
设函数f(x)=sin3x+|sin3x|,则f(x)为( )
A.周期函数,最小正周期为
| ||
B.周期函数,最小正周期为
| ||
| C.周期函数,数小正周期为2π | ||
| D.非周期函数 |
先将周期最小的选项A和C的周期T=
和2π代入f(x+
)=-sin3x+|sin3x|≠f(x),f(x+2π)=-sin3x+|sin3x|≠f(x),故排除A和C;
再检验(B)f(x+
)=sinx+|sin3x|=f(x),成立,可推断函数为周期函数排除D.
故选B
| π |
| 3 |
| π |
| 3 |
再检验(B)f(x+
| 2π |
| 3 |
故选B

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
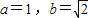 ,
,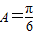 则
则 ;③设二次函数f(x)=x2+ax+a,则“
;③设二次函数f(x)=x2+ax+a,则“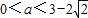 ”是“方程f(x)-x=0的两根x1和x2满足0<x1<x2<1”的充分必要条件.④过点(
”是“方程f(x)-x=0的两根x1和x2满足0<x1<x2<1”的充分必要条件.④过点( ,1)且与函数y=
,1)且与函数y=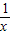 的图象相切的直线方程是4x+y-3=0.其中所有正确说法的序号是 .
的图象相切的直线方程是4x+y-3=0.其中所有正确说法的序号是 .