题目内容
设平面上A、B两点坐标分别是(-cos
,sin
) ,(cos
,sin
) . α∈[0,
],
(1)求|
|的最大值和最小值;
(2)设函数f(x)=
2+4a|
|-3,a∈R,求f(x)的最小值.
| α |
| 2 |
| α |
| 2 |
| 3α |
| 2 |
| 3α |
| 2 |
| π |
| 2 |
(1)求|
| AB |
(2)设函数f(x)=
| AB |
| AB |
分析:(1)由题意可得
的坐标,再根据向量的模的定义求得|
|2=2+2cos2α.再由α∈[0,
],可得cos2α∈[-1,1],由此可得|
|取得最大值和最小值.
(2)由于函数 f(x)=4(cosα+a)2-3-4a2,α∈[0,
],分当a>0时、当-1≤a≤0时、当a<-1时三种情况,分别利用二次函数的性质求得f(x)的最小值.
| AB |
| AB |
| π |
| 2 |
| AB |
(2)由于函数 f(x)=4(cosα+a)2-3-4a2,α∈[0,
| π |
| 2 |
解答:解:(1)由题意可得
=(cos
+cos
,sin
-sin
),
∴|
|2=(cos
+coa
)2+(sin
-sin
)2=2+2cos2α,由α∈[0,
],可得cos2α∈[-1,1],
∴当cos2α=-1时,|
|取得最小值为0,当cos2α=1时,|
|取得最大值为2.
(2)由于函数f(x)=|
|2+4a|
|-3=2+2cos2α+4a
,α∈[0,
],
∴f(x)=4cos2α+8acosα-3=4(cosα+a)2-3-4a2.
当a>0时,则cosα=0时,函数f(x)取得最小值为-3;
当-1≤a≤0时,则cosα=a时,函数f(x)取得最小值为-3-4a2;
当a<-1时,则cosα=1时,f(x)取得最小值为1+8a.
| AB |
| 3α |
| 2 |
| α |
| 2 |
| 3α |
| 2 |
| α |
| 2 |
∴|
| AB |
| 3α |
| 2 |
| α |
| 2 |
| 3α |
| 2 |
| α |
| 2 |
| π |
| 2 |
∴当cos2α=-1时,|
| AB |
| AB |
(2)由于函数f(x)=|
| AB |
| AB |
| 2+2cos2α |
| π |
| 2 |
∴f(x)=4cos2α+8acosα-3=4(cosα+a)2-3-4a2.
当a>0时,则cosα=0时,函数f(x)取得最小值为-3;
当-1≤a≤0时,则cosα=a时,函数f(x)取得最小值为-3-4a2;
当a<-1时,则cosα=1时,f(x)取得最小值为1+8a.
点评:本题主要考查求向量的模,三角函数的恒等变换、二次函数在闭区间上的最值,属于中档题.

练习册系列答案
相关题目
 ,是两个非零向量,如果
,是两个非零向量,如果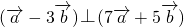 ,且
,且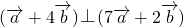 ,求向量
,求向量 与
与 的夹角大小;
的夹角大小;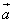 ,
,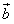 是两个非零向量,如果
是两个非零向量,如果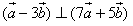 ,且
,且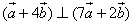 ,求向量
,求向量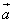 与
与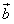 的夹角大小;
的夹角大小;