题目内容
如图,F是抛物线y2=2px(p>0)的焦点,Q是准线与x轴的交点,斜率为k的直线l经过点Q.(1)当K取不同数值时,求直线l与抛物线交点的个数;
(2)如直线l与抛物线相交于A、B两点,求证:KFA+KFB是定值
(3)在x轴上是否存在这样的定点M,对任意的过点Q的直线l,如l
与抛物线相交于A、B两点,均能使得kMA•kMB为定值,有则找出满足条
件的点M;没有,则说明理由.

【答案】分析:(1)设 代入y2=2px,得:
代入y2=2px,得: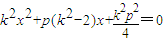 ,
,
然后结合k的取值和根的判别式求直线l与抛物线交点的个数.
(2)设交点A(x1,y1),B(x2,y2),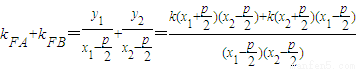 ,
,
由此可求出KFA+KFB是定值0.
(3)如存在满足条件的点M(t,0),
使得KMA•KMB= ,
,
仅当t=0,即M(0,0)时,KMA•KMB=4.
解答:解:(1)设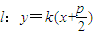 代入y2=2px
代入y2=2px
得: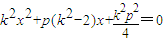 (*)1k=0,一个交点,2k≠0,△=-4p2(k2-1),
(*)1k=0,一个交点,2k≠0,△=-4p2(k2-1),
△>0,即k∈(-1,0)∪(0,1)两个交点
△=0,k=±1时一个交点
△<0,k<-1或k>1无交点
(2)设交点A(x1,y1),B(x2,y2),
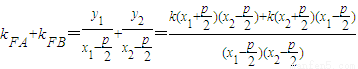 =
=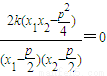 ,
,
斜率和为定值0
(3)如存在满足条件的点M(t,0),使得KMA•KMB为定值,
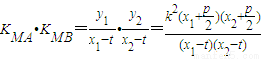 =
=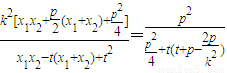
仅当t=0,即M(0,0)时,KMA•KMB=4
点评:本题考查椭圆的性质及其综合运用,解题时要注意公式的灵活运用.
 代入y2=2px,得:
代入y2=2px,得: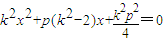 ,
,然后结合k的取值和根的判别式求直线l与抛物线交点的个数.
(2)设交点A(x1,y1),B(x2,y2),
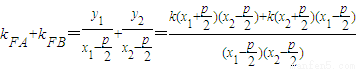 ,
,由此可求出KFA+KFB是定值0.
(3)如存在满足条件的点M(t,0),
使得KMA•KMB=
 ,
,仅当t=0,即M(0,0)时,KMA•KMB=4.
解答:解:(1)设
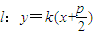 代入y2=2px
代入y2=2px得:
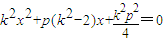 (*)1k=0,一个交点,2k≠0,△=-4p2(k2-1),
(*)1k=0,一个交点,2k≠0,△=-4p2(k2-1),△>0,即k∈(-1,0)∪(0,1)两个交点
△=0,k=±1时一个交点
△<0,k<-1或k>1无交点
(2)设交点A(x1,y1),B(x2,y2),
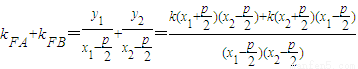 =
=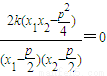 ,
,斜率和为定值0
(3)如存在满足条件的点M(t,0),使得KMA•KMB为定值,
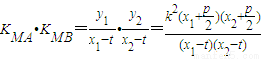 =
=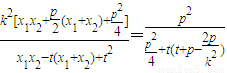
仅当t=0,即M(0,0)时,KMA•KMB=4
点评:本题考查椭圆的性质及其综合运用,解题时要注意公式的灵活运用.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
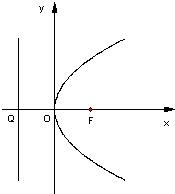 如图,F是抛物线y2=2px(p>0)的焦点,Q是准线与x轴的交点,斜率为k的直线l经过点Q.
如图,F是抛物线y2=2px(p>0)的焦点,Q是准线与x轴的交点,斜率为k的直线l经过点Q. 如图,F是抛物线y2=4x的焦点,Q是准线与x轴的交点,直线l经过点Q.
如图,F是抛物线y2=4x的焦点,Q是准线与x轴的交点,直线l经过点Q.
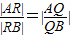 ,求点R的轨迹方程.
,求点R的轨迹方程.