题目内容
如图,F是抛物线y2=4x的焦点,Q是准线与x轴的交点,直线l经过点Q.(Ⅰ)直线l与抛物线有唯一公共点,求l方程;
(Ⅱ)直线l与抛物线交于A、B两点;(i)设FA、FB的斜率分别为k1,k2,求k1+k2的值;
(ii)若点R在线段AB上,且满足
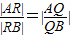 ,求点R的轨迹方程.
,求点R的轨迹方程.
【答案】分析:设l的方程为y=k(x+1),代入抛物线方程,可得k2x2+(2k2-4)x+k2=0,利用直线l与抛物线有唯一公共点
(1)若k≠0,令△=0得,k=±1,此时l的方程为y=x+1或y=-x-1;若k=0,方程有唯一解,此时l的方程为y=0;
(2)( i)显然k≠0,令A(x1,y1),B(x2,y2),则利用韦达定理及斜率公式可求k1+k2的值;
( ii)设点R的坐标为(x,y).利用 ,即可得到
,即可得到 ,
, ,由此可得点R的轨迹方程.
,由此可得点R的轨迹方程.
解答:解:由题意,Q(-1,0),直线l斜率存在,设其斜率为k,则l的方程为y=k(x+1),
代入抛物线方程,可得k2x2+(2k2-4)x+k2=0
(1)若k≠0,令△=0,得k=±1,此时l的方程为y=x+1或y=-x-1;
若k=0,方程有唯一解,此时l的方程为y=0;
(2)显然k≠0,令A(x1,y1),B(x2,y2),则
 ,x1x2=1,
,x1x2=1, ,
, (7分)
(7分)
( i) (9分)
(9分)
( ii)设点R的坐标为(x,y)
∵ ,∴
,∴ ,
,
∴ ,
, ,(12分)
,(12分)
由△>0得,-1<k<1,又k≠0,
∴y∈(-2,0)∪(0,2),
综上所述,点R的轨迹方程为x=1(y∈(-2,0)∪(0,2))(14分)
点评:本题考查轨迹方程的求解,考查直线与抛物线的位置关系,注意分类讨论是关键.
(1)若k≠0,令△=0得,k=±1,此时l的方程为y=x+1或y=-x-1;若k=0,方程有唯一解,此时l的方程为y=0;
(2)( i)显然k≠0,令A(x1,y1),B(x2,y2),则利用韦达定理及斜率公式可求k1+k2的值;
( ii)设点R的坐标为(x,y).利用
 ,即可得到
,即可得到 ,
, ,由此可得点R的轨迹方程.
,由此可得点R的轨迹方程.解答:解:由题意,Q(-1,0),直线l斜率存在,设其斜率为k,则l的方程为y=k(x+1),
代入抛物线方程,可得k2x2+(2k2-4)x+k2=0
(1)若k≠0,令△=0,得k=±1,此时l的方程为y=x+1或y=-x-1;
若k=0,方程有唯一解,此时l的方程为y=0;
(2)显然k≠0,令A(x1,y1),B(x2,y2),则
 ,x1x2=1,
,x1x2=1, ,
, (7分)
(7分)( i)
 (9分)
(9分)( ii)设点R的坐标为(x,y)
∵
 ,∴
,∴ ,
,∴
 ,
, ,(12分)
,(12分)由△>0得,-1<k<1,又k≠0,
∴y∈(-2,0)∪(0,2),
综上所述,点R的轨迹方程为x=1(y∈(-2,0)∪(0,2))(14分)
点评:本题考查轨迹方程的求解,考查直线与抛物线的位置关系,注意分类讨论是关键.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
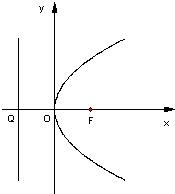 如图,F是抛物线y2=2px(p>0)的焦点,Q是准线与x轴的交点,斜率为k的直线l经过点Q.
如图,F是抛物线y2=2px(p>0)的焦点,Q是准线与x轴的交点,斜率为k的直线l经过点Q. 如图,F是抛物线y2=4x的焦点,Q是准线与x轴的交点,直线l经过点Q.
如图,F是抛物线y2=4x的焦点,Q是准线与x轴的交点,直线l经过点Q.
