题目内容
2.袋子中装有大小相同的6个小球,2红4白,现从中有放回的随机摸球3次,每次摸出1个小球,则至少有2次摸出白球的概率为( )| A. | $\frac{20}{27}$ | B. | $\frac{2}{3}$ | C. | $\frac{16}{27}$ | D. | $\frac{7}{9}$ |
分析 每次摸到红球的概率都是$\frac{1}{3}$,摸到白球的概率都是$\frac{2}{3}$,由此利用n次独立重复试验中事件A恰好发生k次的概率计算公式能求出至少有2次摸出白球的概率.
解答 解:∵袋子中装有大小相同的6个小球,2红4白,现从中有放回的随机摸球3次,每次摸出1个小球,
∴每次摸到红球的概率都是$\frac{1}{3}$,摸到白球的概率都是$\frac{2}{3}$,
∴至少有2次摸出白球的概率为:
p=${C}_{3}^{2}(\frac{1}{3})(\frac{2}{3})^{2}+{C}_{3}^{3}(\frac{2}{3})^{3}$=$\frac{20}{27}$.
故选:A.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意n次独立重复试验中事件A恰好发生k次的概率计算公式的合理运用.

练习册系列答案
相关题目
7.复数i(3-i)的共轭复数是( )
| A. | 1+3i | B. | 1-3i | C. | -1+3i | D. | -1-3i |
14.如果a>b,那么下列不等式中正确的是( )
| A. | $\frac{1}{a}>\frac{1}{b}$ | B. | a2>b2 | C. | lg(|a|+1)>lg(|b|+1) | D. | 2a>2b |
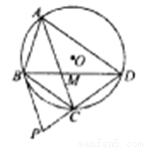
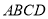 为圆
为圆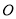 的内接四边形,且
的内接四边形,且 ,其对角线
,其对角线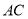 与
与 相交于点
相交于点 ,过点
,过点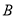 作圆
作圆 的切线交
的切线交 的延长线于点
的延长线于点 .
.
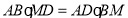 ;
;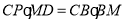 ,求证:
,求证: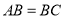 .
. 满足
满足 ,则
,则 的取值范围为( )
的取值范围为( ) B.
B.
 D.
D.
 是定义在
是定义在 上的可导函数,其导函数为
上的可导函数,其导函数为 ,且有
,且有 ,则不等式
,则不等式 的解集为( )
的解集为( ) B.
B. C.
C. D.
D.
 ( )
( ) B.
B. C.
C. D.
D.