题目内容

由曲线f（x）=
x
与y轴及直线y=m（m＞0）围成的图形面积为
8
3
，则m的值为
2
2
．
分析：联立
y=m
y=
x
解得交点，进而利用定积分解出即可．
解答：解：联立
y=m
y=
x
解得
x=m2
y=m
，即交点为（m2，m），
由题意得
∫
m2
0
(m-
x
)dx=
8
3
，
∴(mx-
2
3
x
3
2
)
|
m2
0
=
8
3
，解得m=2．
故答案为2．
点评：利用定积分求面积是求面积的通法，应熟练掌握．
练习册系列答案
相关题目
由曲线f（x）=
x
与x轴及直线x=m（m＞0）围成的图形面积为
16
3
，则m的值为
4
4
．
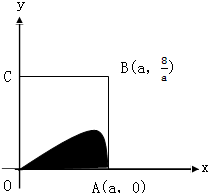如图，矩形OABC内的阴影部分由曲线f（x）=sinx（x∈（0，π））及直线x=a（a∈（0，π））与x轴围成，向矩形OABC内随机投掷一点，若落在阴影部分的概率为
3
16
，则a的值为（　　）
由曲线f（x）=ex与直线y=1，x=1所围成的图形面积是（　　）
由曲线f（x）=
x
与y轴及直线y=m（m＞0）围成的图形面积为
8
3
，则m的值为______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网