题目内容
9．甲、乙两名同学互不影响地在同一位置投球，每次命中率分别为$\frac{1}{2}$与$\frac{1}{3}$．若甲、乙两人各投球1次，则恰有一人投中的概率为$\frac{1}{2}$．分析 恰有一人投中是指甲中乙不中或甲不中乙中，由此利用相互独立事件概率加法公式和互斥事件概率乘法公式能求出恰有一人投中的概率．
解答 解：∵甲、乙两名同学互不影响地在同一位置投球，每次命中率分别为$\frac{1}{2}$与$\frac{1}{3}$，
∴甲、乙两人各投球1次，则恰有一人投中的概率为：
p=$\frac{1}{2}×（1-\frac{1}{3}）+（1-\frac{1}{2}）×\frac{1}{3}$=$\frac{1}{2}$．
故答案为：$\frac{1}{2}$．
点评 本题考查概率的求法，是基础题，解题时要认真审题，注意相互独立事件概率加法公式和互斥事件概率乘法公式的合理运用．
练习册系列答案
心算口算巧算一课一练系列答案
应用题作业本系列答案
相关题目
20．在△ABC中，内角A、B、C所对的边分别为a、b、c，且$\frac{2a+b}{c}$=$\frac{cos（A+C）}{cosC}$，c=2，则△ABC面积的最大值为（ ）
| A． | $\frac{{\sqrt{3}}}{3}$ | B． | $\frac{3}{4}$ | C． | $\frac{{3\sqrt{3}}}{4}$ | D． | $2\sqrt{3}$ |
17．已知集合M={x|y=ln（1-x）}，集合N={y|y=3x，x∈R}，则M∩N=（ ）
| A． | {x|x＜1} | B． | {x|x＞1} | C． | {x|0＜x＜1} | D． | ∅ |
14．根据如表样本数据，
得到了回归直线方程：$\widehat{y}$=bx+a，则（ ）
| x | 3 | 4 | 5 | 6 | 7 | 8 |
| y | 4 | 2.5 | -0.5 | -1 | -2 | -3 |
| A． | a＞0，b＞0 | B． | a＜0，b＞0 | C． | a＞0，b＜0 | D． | a＜0，b＜0 |
1．某班倡议假期每位学生至少阅读一本名著，为了解学生的阅读情况，对该班所有学生进行了调查．调查结果如表：
（Ⅰ）试根据上述数据，求这个班级女生阅读名著的平均本数；
（Ⅱ）若从阅读5本名著的学生中任选2人交流读书心得，求选到男生和女生各1人的概率．
| 阅读名著的本数 | 1 | 2 | 3 | 4 | 5 |
| 男生人数 | 3 | 1 | 2 | 1 | 3 |
| 女生人数 | 1 | 3 | 3 | 1 | 2 |
（Ⅱ）若从阅读5本名著的学生中任选2人交流读书心得，求选到男生和女生各1人的概率．
18．设集合A={x|（x-1）（x-2）2=0}，则集合A中元素的个数为（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
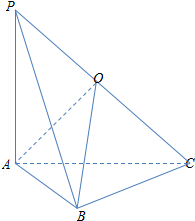如图，已知三棱锥P-ABC中，PA⊥平面ABC，AB⊥BC，且AB=BC=1，PA=$\sqrt{2}$，O为线段PC的中点，