题目内容
已知函数
，讨论
的单调性．
【解析】由已知，得的定义域为
∴
由
得
，
（1）当
即
时，
，此时，在上是增函数；
（2）当
，即
时，
令
，解得
或
；令
，解得
此时在
上递增，在
上递减，在
上递增
（3）当
，即
或
时
令，解得
或
；令，解得
此时在
上递增，在
上递减，在
上递增
综上所述：当
时，在上是增函数；当时，在上递增，在上递减，在上递增；当或时，在上递增，在上递减，在上递增.
练习册系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
，且
，那么
的取值范围是 ．
， 则
（ ） 
B。
C。
D。
．
圆
与圆
外切，求动圆圆心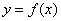
的图象如图2所示，则其导函数
的图象可能是（ ）
的单调递减区间为( )
满足
，
，求
