题目内容
（2013•浙江）在锐角△ABC中，内角A，B，C的对边分别为a，b，c，且2asinB=
b．
（Ⅰ）求角A的大小；
（Ⅱ）若a=6，b+c=8，求△ABC的面积．
b．（Ⅰ）求角A的大小；
（Ⅱ）若a=6，b+c=8，求△ABC的面积．
（1）
（2）
（2）（Ⅰ）由2asinB=
b，利用正弦定理得：2sinAsinB=sinB，
∵sinB≠0，∴sinA=
，
又A为锐角，
则A=；
（Ⅱ）由余弦定理得：a2=b2+c2﹣2bc•cosA，即36=b2+c2﹣bc=（b+c）2﹣3bc=64﹣3bc，
∴bc=
，又sinA=，
则S△ABC=
bcsinA=．
b，利用正弦定理得：2sinAsinB=sinB，∵sinB≠0，∴sinA=
，又A为锐角，
则A=
；（Ⅱ）由余弦定理得：a2=b2+c2﹣2bc•cosA，即36=b2+c2﹣bc=（b+c）2﹣3bc=64﹣3bc，
∴bc=
，又sinA=，则S△ABC=
bcsinA=．
练习册系列答案
轻松课堂单元测试AB卷系列答案
小题狂做系列答案
相关题目
中，内角
的对边分别为
，且
．
的值； 
，
，求
的面积．
中，
，
，
，若点
满足
，且
，则
＝ ．
中，
,
,
，则
边上的高等于（ ）
，
＝2，且S△ABC＝
， 则b的值为( )
＋
的取值范围为______．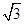
，b＝1，c＝2，则A等于____________．
的三个内角
所对的边分别为
．若△
的面积
，则
的值是 。
的内角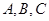
所对的边分别为
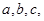且
，则角
；