题目内容
5.已知函数$f(x)=\sqrt{3}sin2x+cos2x+3$.(Ⅰ)求f(x)的最小正周期与单调递增区间;
(Ⅱ)在△ABC中,a,b,c分别是角A,B,C的对边,若$a=\sqrt{3}$,f(A)=4,求b+c的值.
分析 (I)f(x)=$2(\frac{\sqrt{3}}{2}sin2x+\frac{1}{2}cos2x)$+3=$2sin(2x+\frac{π}{6})$+3,利用正弦函数的周期性与单调性即可得出.
(II)由f(A)=4,可得:$2sin(2A+\frac{π}{6})$+3=4,化为$sin(2A+\frac{π}{6})$=$\frac{1}{2}$,利用0<A<π,可得$2A+\frac{π}{6}$=$\frac{5π}{6}$,解得A值.可得B+C=$\frac{2π}{3}$.由正弦定理可得:b+c=2(sinB+sinC)=$2\sqrt{3}sin(B+\frac{π}{6})$,即可得出.
解答 解:(I)f(x)=$2(\frac{\sqrt{3}}{2}sin2x+\frac{1}{2}cos2x)$+3=$2sin(2x+\frac{π}{6})$+3,
∴f(x)的最小正周期T=$\frac{2π}{2}$=π.
由$2kπ-\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,解得kπ-$\frac{π}{3}$≤x≤kπ+$\frac{π}{6}$,(k∈Z),
∴函数f(x)的单调递增区间为$[kπ-\frac{π}{3},\frac{π}{6}+kπ]$,(k∈Z).
(II)由f(A)=4,可得:$2sin(2A+\frac{π}{6})$+3=4,化为$sin(2A+\frac{π}{6})$=$\frac{1}{2}$,
∵0<A<π,∴$\frac{π}{6}$<2A+$\frac{π}{6}$<$\frac{13π}{6}$,
∴$2A+\frac{π}{6}$=$\frac{5π}{6}$,解得A=$\frac{π}{3}$.∴B+C=$\frac{2π}{3}$.
由正弦定理可得:$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}$=$\frac{\sqrt{3}}{sin\frac{π}{3}}$=2.
∴b+c=2(sinB+sinC)=2(sinB+sin$(\frac{π}{3}+B)$)=$2\sqrt{3}sin(B+\frac{π}{6})$$≤2\sqrt{3}$.
点评 本题考查了和差公式、三角函数的图象与性质、三角函数求值、正弦定理,考查了推理能力与计算能力,属于中档题.

| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | 2π |
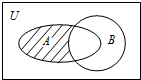 已知全集U=R,集合$A=\{\;x|\;{(\frac{1}{2})^x}≤1\;\}$,B={x|x2-6x+8≤0},则图中阴影部分所表示的集合为( )
已知全集U=R,集合$A=\{\;x|\;{(\frac{1}{2})^x}≤1\;\}$,B={x|x2-6x+8≤0},则图中阴影部分所表示的集合为( )| A. | {x|x≤0} | B. | {x|2≤x≤4} | C. | {x|0<x≤2或x≥4} | D. | {x|0≤x<2或x>4} |
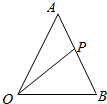 如图,在△OAB中,点P为线段AB上的一个动点(不包含端点),且满足$\overrightarrow{AP}$=λ$\overrightarrow{PB}$.
如图,在△OAB中,点P为线段AB上的一个动点(不包含端点),且满足$\overrightarrow{AP}$=λ$\overrightarrow{PB}$.