题目内容
已知函数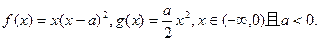
(I)(i)求函数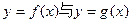 的图象的交点A的坐标;
的图象的交点A的坐标;
(ii)设函数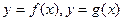 的图象在交点A处的切线分别为
的图象在交点A处的切线分别为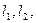 是否存在这样的实数a,使得
是否存在这样的实数a,使得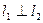 ?若存在,请求出a的值和相应的点A坐标;若不存在,请说明理由。
?若存在,请求出a的值和相应的点A坐标;若不存在,请说明理由。
(II)记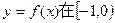 上最小值为F(a),求
上最小值为F(a),求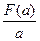 的最小值。
的最小值。
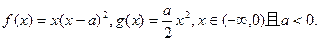
(I)(i)求函数
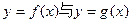 的图象的交点A的坐标;
的图象的交点A的坐标;(ii)设函数
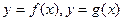 的图象在交点A处的切线分别为
的图象在交点A处的切线分别为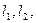 是否存在这样的实数a,使得
是否存在这样的实数a,使得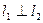 ?若存在,请求出a的值和相应的点A坐标;若不存在,请说明理由。
?若存在,请求出a的值和相应的点A坐标;若不存在,请说明理由。(II)记
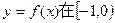 上最小值为F(a),求
上最小值为F(a),求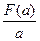 的最小值。
的最小值。(Ⅰ)(i)点A坐标为
(ii) 存在
(Ⅱ)

(ii) 存在

(Ⅱ)

(I)(i)设点A的坐标为
得
故函数 与
与 图象的交点A坐标为
图象的交点A坐标为 3分
3分
(ii) 若存在a,使得
若存在a,使得
则当点A坐标为
又 ,
,
则 ,此时点A坐标为
,此时点A坐标为 5分
5分
当点A坐标为
又 ,
,
则 ,无解。 7分
,无解。 7分
综上,存在
(II)令 整理得
整理得
 图象另一交点横坐标
图象另一交点横坐标
10分

结合图象可得:
(1)若
(2)若
(3)若
综上
所以 13分
13分
当
且当 时取到“=”;
时取到“=”;
当 时,函数
时,函数 单调递减,此时
单调递减,此时
综上, 15分
15分

得

故函数
 与
与 图象的交点A坐标为
图象的交点A坐标为 3分
3分(ii)
 若存在a,使得
若存在a,使得
则当点A坐标为

又
 ,
,则
 ,此时点A坐标为
,此时点A坐标为 5分
5分当点A坐标为

又
 ,
,则
 ,无解。 7分
,无解。 7分综上,存在

(II)令
 整理得
整理得 图象另一交点横坐标
图象另一交点横坐标
10分

结合图象可得:
(1)若

(2)若

(3)若

综上

所以
 13分
13分当

且当
 时取到“=”;
时取到“=”;当
 时,函数
时,函数 单调递减,此时
单调递减,此时
综上,
 15分
15分
练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
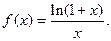
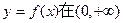 上的单调性;
上的单调性;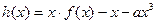 在(0,2)上有极值,求
在(0,2)上有极值,求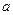 的取值范围。
的取值范围。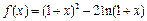 .
.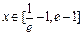 时,不等式f (x)<m恒成立,求实数m的取值范围;
时,不等式f (x)<m恒成立,求实数m的取值范围;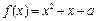 在区间[0, 2]上恰好有两个相异的实根,求实数a的取值范围.
在区间[0, 2]上恰好有两个相异的实根,求实数a的取值范围.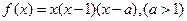
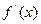 ; 并证明
; 并证明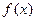 有两个不同的极值点
有两个不同的极值点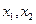 ;
; 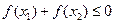 成立,求
成立,求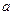 的取值范围.
的取值范围.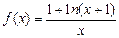
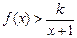 恒成立,求正整数k的最大值.
恒成立,求正整数k的最大值.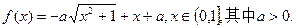
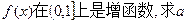 的取值范围;
的取值范围;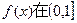 上的最大值.
上的最大值.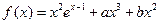 ,已知
,已知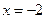 和
和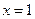 为
为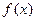 的极值点.
的极值点.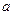 和
和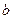 的值;
的值;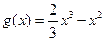 ,比较
,比较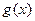 的大小.
的大小.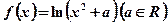 . (1)求在函数
. (1)求在函数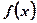 图像上点
图像上点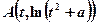 处的切线
处的切线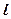 的方程;(2)若切线
的方程;(2)若切线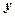 轴上的纵坐标截距记为
轴上的纵坐标截距记为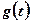 ,讨论
,讨论