题目内容
过点( ,0)引直线l与曲线y=
,0)引直线l与曲线y= 相交于A、B两点,O为坐标原点,当△AOB的面积取最大值时,直线l的斜率等于( ).
相交于A、B两点,O为坐标原点,当△AOB的面积取最大值时,直线l的斜率等于( ).
A. | B.- | C.± | D.- |
B
解析

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
过 的直线
的直线 被圆
被圆 截得的线段长为2时,直线
截得的线段长为2时,直线 的斜率为( )
的斜率为( )
A. | B. | C. | D. |
动圆C经过点 ,并且与直线
,并且与直线 相切,若动圆C与直线
相切,若动圆C与直线 总有公共点,则圆C的面积( )
总有公共点,则圆C的面积( )
A.有最大值 | B.有最小值 | C.有最小值 | D.有最小值 |
圆 的半径为( )
的半径为( )
A. | B. | C. | D. |
已知圆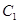 :
: ,圆
,圆 与圆
与圆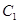 关于直线
关于直线 对称,则圆
对称,则圆 的方程为 ( )
的方程为 ( )
A. | B. |
C. | D. |
已知圆C1:(x-2)2+(y-3)2=1,圆C2:(x-3)2+(y-4)2=9,M,N分别是圆C1,C2上的动点,P为x轴上的动点,则|PM|+|PN|的最小值为( )
A.5 -4 -4 | B. -1 -1 |
C.6-2 | D. |
圆(x+2)2+y2=4与圆(x-2)2+(y-1)2=9的位置关系为( ).
| A.内切 | B.相交 |
| C.外切 | D.相离 |
若圆C的半径为1,圆心在第一象限,且与直线4x-3y=0和x轴都相切,则该圆的标准方程是( ).
A.(x-3)2+ 2=1 2=1 |
B.(x-2)2+ 2=1 2=1 |
C.(x-1)2+ 2=1 2=1 |
D. 2+(y-1)2=1 2+(y-1)2=1 |
过点A(1,-1),B(-1,1),且圆心在直线x+y-2=0上的圆的方程是 ( ).
| A.(x-3)2+(y+1)2=4 | B.(x+3)2+(y-1)2=4 |
| C.(x-1)2+(y-1)2=4 | D.(x+1)2+(y+1)2=4 |