题目内容
过
的直线
被圆
截得的线段长为2时，直线的斜率为（ ）
A． | B． | C． | D． |
A
解析试题分析：由题意直线的斜率存在设为
，则直线的方程为
，即
由点到直线的距离公式得，圆心到直线的距离为
，由圆的性质可得
，即
，解得
，即
．
考点：直线与圆的位置关系．
练习册系列答案
相关题目
在点
处的切线为
，则直线
上的任意点Q之间的最近距离是（ ）
圆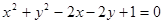
上的点到直线
的距离最大值是( )
| A．2 | B．1+ | C． | D．1+ |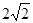
点
在圆
的内部，则
的取值范围是（ ）
A． | B． | C． | D． |
如果直线
将圆
平分且不通过第四象限，则的斜率的取值范围是（ ）
A． | B． | C． | D． |
已知圆心(a，b)(a<0，b<0)在直线y＝2x＋1上的圆，其圆心到x轴的距离恰好等于圆的半径，在y轴上截得的弦长为2
，则圆的方程为( )
| A．(x＋2)2＋(y＋3)2＝9 | B．(x＋3)2＋(y＋5)2＝25 |
C．(x＋6)2＋ 2＝ | D． 2＋2＝ |
若直线3x+y+a=0过圆x2+y2+2x-4y=0的圆心,则a的值为( )
| A．-1 | B．1 | C．3 | D．-3 |
当a为任意实数时,直线(a-1)x-y+a+1=0恒过定点C,则以C为圆心,
为半径的圆的方程为( )
| A．x2+y2-2x+4y=0 | B．x2+y2+2x+4y=0 |
| C．x2+y2+2x-4y=0 | D．x2+y2-2x-4y=0 |
，0)引直线l与曲线y＝
相交于A、B两点，O为坐标原点，当△AOB的面积取最大值时，直线l的斜率等于( )．
