题目内容
已知tanθ=2,
(1)求
值;
(2)3sin2α+5sinα×cosα-3值.
(1)求
| 2sinα+3cosα |
| 3sinα-4cosα |
(2)3sin2α+5sinα×cosα-3值.
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:(1)原式分子分母除以cosα,利用同角三角函数间基本关系化简,把tanα的值代入计算即可求出值;
(2)原式分母看做“1”,利用同角三角函数间基本关系化简,把tanα的值代入计算即可求出值.
(2)原式分母看做“1”,利用同角三角函数间基本关系化简,把tanα的值代入计算即可求出值.
解答:
解:(1)∵tanα=2,
∴原式=
=
=
;
(2)∵tanα=2,
∴原式=
=
=
=
.
∴原式=
| 2tanα+3 |
| 3tanα-4 |
| 4+3 |
| 6-4 |
| 7 |
| 2 |
(2)∵tanα=2,
∴原式=
| 11sinαcosα-3sin2α-3cos2α |
| sin2α+cos2α |
| 11tanα-3tan2α-3 |
| tan2α+1 |
| 22-12-3 |
| 4+1 |
| 7 |
| 5 |
点评:此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若a>1,则函数y=(
)•ax的图象的基本形状是( )
| x |
| |x| |
A、 |
B、 |
C、 |
D、 |
已知全集U={0,1,2,3,4},集合A={0,1,2,3},B={0,3,4},则A∩∁UB=( )
| A、{2,4} |
| B、{1,2} |
| C、{0,1} |
| D、{0,1,2,3} |
若函数y=lg(9-a•3x)的定义域为R,则实数a的取值范围是( )
| A、(0,+∞) |
| B、(0,2) |
| C、(-∞,2) |
| D、(-∞,0] |
如果集合A={x|x≤1},则下面式子正确的是( )
| A、0⊆A | B、{0}∈A |
| C、φ∈A | D、{0}⊆A |
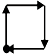
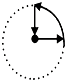
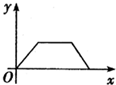 如图是王珊早晨离开家边走边背诵英语过程中离家距离y与行走时间x之间函数关系的图象.若用黑点表示王珊家的位置,则王珊步行走的路线可能是( )
如图是王珊早晨离开家边走边背诵英语过程中离家距离y与行走时间x之间函数关系的图象.若用黑点表示王珊家的位置,则王珊步行走的路线可能是( )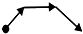

 已知A,B分别是椭圆C:
已知A,B分别是椭圆C: