题目内容
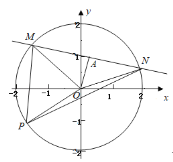
【题目】直线![]() 与圆
与圆![]() 相交于两点
相交于两点![]() ,若
,若![]() ,
,![]() 为圆
为圆![]() 上任意一点,则
上任意一点,则![]() 的取值范围是______.
的取值范围是______.
【答案】![]()
【解析】
取MN的中点A,连接OA,则OA⊥MN.算出OA=1,得到∠AON,可得∠MON,计算出![]()
![]() 的值,运用向量的加减运算和向量数量积的定义,可得
的值,运用向量的加减运算和向量数量积的定义,可得![]() 2﹣4cos∠AOP,考虑
2﹣4cos∠AOP,考虑![]() ,
,![]() 同向和反向,可得最值,即可得到所求范围.
同向和反向,可得最值,即可得到所求范围.
取MN的中点A,连接OA,则OA⊥MN,
∵c2=a2+b2,
∴O点到直线MN的距离OA![]() 1,
1,
x2+y2=4的半径r=2,
∴Rt△AON中,设∠AON=θ,得cosθ![]() ,得θ=
,得θ=![]() ,
,
cos∠MON=cos2θ=![]() ,
,
由此可得,![]()
![]() |
|![]() ||
||![]() |cos∠MON
|cos∠MON
=2×2×(![]() )=﹣2,
)=﹣2,
则![]() (
(![]() )(
)(![]() )
)![]()
![]() 2
2![]() (
(![]() )
)
=﹣2+4﹣2![]()
![]() 2﹣2|
2﹣2|![]() ||
||![]() |cos∠AOP=2﹣4cos∠AOP,
|cos∠AOP=2﹣4cos∠AOP,
当![]() ,
,![]() 同向时,取得最小值且为2﹣4=﹣2,
同向时,取得最小值且为2﹣4=﹣2,
当![]() ,
,![]() 反向时,取得最大值且为2+4=6.
反向时,取得最大值且为2+4=6.
则![]() 的取值范围是
的取值范围是![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目