题目内容
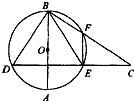（几何证明选讲）如图，⊙O中，直径AB和弦DE互相垂直，C是DE延长线上一点，连接BC与圆O交于F，若∠CFE=40°则∠DEB=
40°
40°
．分析：由题意可得，AB垂直平分DE，从而可得∠D=∠BED，由DEFB四点共圆可得∠EFC=∠D=40°．
解答：解：∵直径AB和弦DE互相垂直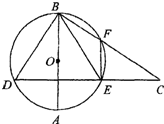
∴AB平分DE
∴BD=BE，∠D=∠BED
∵DEFB四点共圆
∴∠EFC=∠D=40°．
∴∠DEB=40°．
故答案为：40°．
∴AB平分DE
∴BD=BE，∠D=∠BED
∵DEFB四点共圆
∴∠EFC=∠D=40°．
∴∠DEB=40°．
故答案为：40°．
点评：本题主要考查了垂径定理及四点共圆性质定理的应用，属于基础试题．
练习册系列答案
名校课堂系列答案
相关题目
（选修4-1：几何证明选讲）
（几何证明选讲）如图，AB、CD是圆O的两条弦，且AB是线段CD的中垂线，已知AB=10，CD=8，则线段AC的长度为
（1）几何证明选讲：如图，CB是⊙O的直径，AP是⊙O的切线，A为切点，AP与CB的延长线交于点P，若PA=8，PB=4，求AC的长度．
选修4-1：几何证明选讲．
（1）（几何证明选讲）如图，AB是半圆O的直径，点C在半圆上，CD⊥AB，垂足为D，且AD=5DB，设∠COD=θ，则tanθ的值为