题目内容
已知圆O: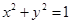 和定点A(2,1),由圆O外一点
和定点A(2,1),由圆O外一点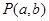 向圆O引切线PQ,切点为Q,且满足
向圆O引切线PQ,切点为Q,且满足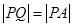
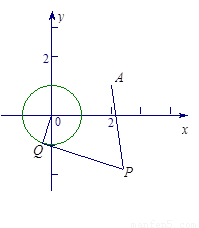
(1) 求实数a、b间满足的等量关系;
(2) 若以P为圆心所作的圆P与圆O有公共点,试求半径取最小值时圆P的方程.
【答案】
(1) ;(2)
;(2)  。
。
【解析】

试题分析:(1)连
 为切点,
为切点, ,由勾股定理有
,由勾股定理有
 .
.
又由已知 ,故
,故
即: .
.
化简得: .
.
(2)设圆 的半径为
的半径为 ,
,
 圆
圆 与圆O有公共点,且半径最小,
与圆O有公共点,且半径最小,

 ,
,
故当 时,
时,
此时,  ,
, .
.
得半径取最小值时圆 的方程为
的方程为 .
.
另解: 圆 与圆O有公共点,圆
与圆O有公共点,圆 半径最小时为与圆O外切的情形,而这些半径的最小值为圆心
半径最小时为与圆O外切的情形,而这些半径的最小值为圆心 到直线
到直线 的距离减去
的距离减去 ,圆心为
,圆心为 过原点与
过原点与 垂直的直线
垂直的直线 与
与 的交点
的交点 .
.
 =
-1 = -1.
=
-1 = -1.
又  :x-2y = 0,
:x-2y = 0,
解方程组 ,得
,得 .即
.即 (
,).
(
,).
∴ 所求圆方程为 .
.
考点:圆的方程;两点间的距离公式;直线与圆的综合应用。
点评:此题主要考查了圆的标准方程,两点间的距离公式,以及二次函数的性质,熟练掌握公式及性质是解本题的关键.

练习册系列答案
相关题目
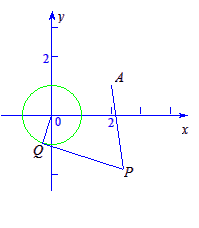
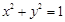 和定点A(2,1),
和定点A(2,1), 向圆O引切线PQ,切点为Q,且满足
向圆O引切线PQ,切点为Q,且满足 .(1) 求实数a、b间满足的等量关系;
.(1) 求实数a、b间满足的等量关系;
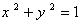 和定点A(2,1),由圆O外一点P(a,b)向圆O引切线PQ,切点为Q,且满足|PQ|=|PA|,
和定点A(2,1),由圆O外一点P(a,b)向圆O引切线PQ,切点为Q,且满足|PQ|=|PA|,