题目内容
如图：已知圆O：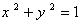
和定点A（2，1），由圆O外一点P(a，b)向圆O引切线PQ，切点为Q，且满足|PQ|=|PA|，
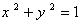和定点A（2，1），由圆O外一点P(a，b)向圆O引切线PQ，切点为Q，且满足|PQ|=|PA|，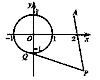 
（1）求实数a，b间满足的等量关系式；
（2）求线段PQ长的最小。
（2）求线段PQ长的最小。
解：（1）连接OP，
因为Q为切点，∴PQ⊥OQ，
由勾股定理有，
又由已知|PQ|=|PA|，故|PQ|2=|PA|2，
即
，
化简，得2a+b-3=0。
（2）由2a+b-3=0，得b=-2a+3，
∴
，
故当
时，线段PQ长取最小值
。
因为Q为切点，∴PQ⊥OQ，
由勾股定理有，
又由已知|PQ|=|PA|，故|PQ|2=|PA|2，
即
，化简，得2a+b-3=0。
（2）由2a+b-3=0，得b=-2a+3，
∴
，故当
时，线段PQ长取最小值。 
练习册系列答案
阅读快车系列答案
相关题目
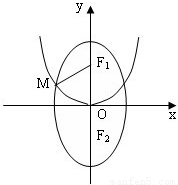
如图，已知F1、F2分别为椭圆
（2013•虹口区一模）已知圆O：x2+y2=4．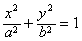
（a> b>0）和圆O：x2+y2=b2，过椭圆上一点P引圆O的两条切线，切点分别为A、B。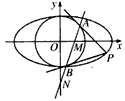
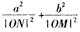为定值。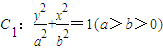
的上、下焦点，其中F1也是抛物线
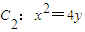的焦点，点M是C1与C2在第二象限的交点，且
．
，
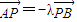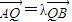（λ≠0且λ≠±1），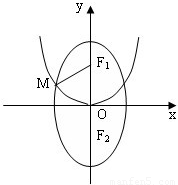
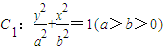的上、下焦点，其中F1也是抛物线
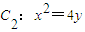的焦点，点M是C1与C2在第二象限的交点，且
．
，
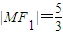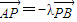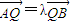（λ≠0且λ≠±1），