题目内容
椭圆 +y2=1上存在一点P,使得它对两个焦点F1,F2的张角∠F1PF2=
+y2=1上存在一点P,使得它对两个焦点F1,F2的张角∠F1PF2= ,则该椭圆的离心率的取值范围是
,则该椭圆的离心率的取值范围是
- A.(0,
 ]
] - B.[
 ,1)
,1) - C.(0,
 ]
] - D.[
 ,1)
,1)
B
分析:首先根据椭圆方程,求出它的离心率为:e= ,然后设点椭圆上P的坐标为(x0,y0),满足∠F1PF2=
,然后设点椭圆上P的坐标为(x0,y0),满足∠F1PF2= ,利用数量积为0列出关于x0、y0和a、c的等式.接下来利用椭圆方程消去y0,得到关于x0的式子,再利用椭圆上点横坐标的范围:-a≤x0≤a,建立关于字母a的不等式,最后解此不等式得出a的范围,代入离心率关于a的表达式,即可得到该椭圆的离心率的取值范围.
,利用数量积为0列出关于x0、y0和a、c的等式.接下来利用椭圆方程消去y0,得到关于x0的式子,再利用椭圆上点横坐标的范围:-a≤x0≤a,建立关于字母a的不等式,最后解此不等式得出a的范围,代入离心率关于a的表达式,即可得到该椭圆的离心率的取值范围.
解答:∵椭圆方程为: +y2=0,
+y2=0,
∴b2=1,可得c2=a2-1,c=
∴椭圆的离心率为e=
又∵椭圆上一点P,使得角∠F1PF2= ,
,
∴设点P的坐标为(x0,y0),结合F1(-c,0),F2(c,0),
可得 =(-c-x0,-y0),
=(-c-x0,-y0), =(c-x0,-y0),
=(c-x0,-y0),
∴
 =
= +
+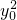 =0…①
=0…①
∵P(x0,y0)在椭圆 +y2=1上,
+y2=1上,
∴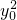 =1-
=1-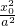 ,代入①可得
,代入①可得 +1-
+1-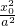 =0
=0
将c2=a2-1代入,得 -a2-
-a2-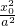 +2=0,所以
+2=0,所以 =
= ,
,
∵-a≤x0≤a
∴ ,即
,即 ,解之得1<a2≤2
,解之得1<a2≤2
∴椭圆的离心率e= =
= ∈[
∈[ ,1).
,1).
点评:本题给出一个特殊的椭圆,在已知椭圆上一点对两个焦点张角为直角的情况下,求椭圆离心率的取值范围,着重考查了椭圆的标准方程和简单几何性质,属于中档题.
分析:首先根据椭圆方程,求出它的离心率为:e=
 ,然后设点椭圆上P的坐标为(x0,y0),满足∠F1PF2=
,然后设点椭圆上P的坐标为(x0,y0),满足∠F1PF2= ,利用数量积为0列出关于x0、y0和a、c的等式.接下来利用椭圆方程消去y0,得到关于x0的式子,再利用椭圆上点横坐标的范围:-a≤x0≤a,建立关于字母a的不等式,最后解此不等式得出a的范围,代入离心率关于a的表达式,即可得到该椭圆的离心率的取值范围.
,利用数量积为0列出关于x0、y0和a、c的等式.接下来利用椭圆方程消去y0,得到关于x0的式子,再利用椭圆上点横坐标的范围:-a≤x0≤a,建立关于字母a的不等式,最后解此不等式得出a的范围,代入离心率关于a的表达式,即可得到该椭圆的离心率的取值范围.解答:∵椭圆方程为:
 +y2=0,
+y2=0,∴b2=1,可得c2=a2-1,c=

∴椭圆的离心率为e=

又∵椭圆上一点P,使得角∠F1PF2=
 ,
,∴设点P的坐标为(x0,y0),结合F1(-c,0),F2(c,0),
可得
 =(-c-x0,-y0),
=(-c-x0,-y0), =(c-x0,-y0),
=(c-x0,-y0),∴

 =
= +
+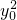 =0…①
=0…①∵P(x0,y0)在椭圆
 +y2=1上,
+y2=1上,∴
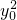 =1-
=1-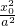 ,代入①可得
,代入①可得 +1-
+1-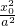 =0
=0将c2=a2-1代入,得
 -a2-
-a2-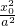 +2=0,所以
+2=0,所以 =
= ,
,∵-a≤x0≤a
∴
 ,即
,即 ,解之得1<a2≤2
,解之得1<a2≤2∴椭圆的离心率e=
 =
= ∈[
∈[ ,1).
,1).点评:本题给出一个特殊的椭圆,在已知椭圆上一点对两个焦点张角为直角的情况下,求椭圆离心率的取值范围,着重考查了椭圆的标准方程和简单几何性质,属于中档题.

练习册系列答案
相关题目
 +y2=1上存在一点P,使得它对两个焦点F1,F2的张角∠F1PF2=
+y2=1上存在一点P,使得它对两个焦点F1,F2的张角∠F1PF2= ,则该椭圆的离心率的取值范围是( )
,则该椭圆的离心率的取值范围是( ) ]
] ,1)
,1) ]
] ,1)
,1) +y2=1上存在一点P,使得它对两个焦点F1,F2的张角∠F1PF2=
+y2=1上存在一点P,使得它对两个焦点F1,F2的张角∠F1PF2= ,则该椭圆的离心率的取值范围是( )
,则该椭圆的离心率的取值范围是( ) ]
] ,1)
,1) ]
] ,1)
,1)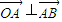 ,点A(4,-3),B点在第一象限且到x轴的距离为5.
,点A(4,-3),B点在第一象限且到x轴的距离为5.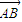 的坐标及OB所在的直线方程;
的坐标及OB所在的直线方程;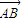 为方向向量且过(0,a)点,问是否存在实数a,使得椭圆
为方向向量且过(0,a)点,问是否存在实数a,使得椭圆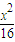 +y2=1上有两个不同的点关于直线l对称.若不存在,请说明理由; 存在请求出实数a的取值范围.
+y2=1上有两个不同的点关于直线l对称.若不存在,请说明理由; 存在请求出实数a的取值范围.