题目内容
4．若3$＜（\frac{1}{3}）$x＜27，则（ ）| A． | -1＜＜3 | B． | -3＜＜-1 | C． | x＜-1或x＞3 | D． | 1＜x＜3 |
分析 根据题意，由3$＜（\frac{1}{3}）$x＜27，可得3＜（3）-x＜33，结合指数函数y=3x为增函数，可得1＜-x＜3，解可得答案．
解答 解：根据题意，由3$＜（\frac{1}{3}）$x＜27，
可得3＜（3）-x＜33，
而指数函数y=3x为增函数，
则必有1＜-x＜3，
即-3＜x＜-1；
故选B．
点评 本题考查指数不等式的解法，注意要分析指数函数的单调性．
练习册系列答案
中考解读考点精练系列答案
相关题目
9．若x，y＞0，且x+2y=1，则（x+$\frac{1}{x}$）（y+$\frac{1}{4y}$）的最小值是（ ）
| A． | $\frac{25}{2}$ | B． | $\frac{25}{4}$ | C． | $\frac{25}{8}$ | D． | $\frac{25}{16}$ |
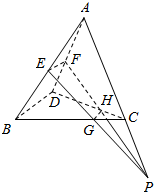已知空间四边形ABCD中，E，F分别是AB，AD的中点，G，H分别是BC，CD上的点，且$\frac{BG}{GC}=\frac{DH}{HC}$=2，求证：直线EG，FH，AC相交于同一点P．