题目内容

已知在△ABC中，三边c＞b＞a，且a、b、c成等差数列，b=2，试求点B的轨迹方程．
考点：轨迹方程
专题：圆锥曲线的定义、性质与方程
分析：b=2，以AC为x轴，线段AB的垂直平分线为y轴，建立直角坐标系．可得A（-1，0），C（1，0）．由于a、b、c成等差数列，可得2b=a+c=4＞|AC|．因此点B的轨迹是椭圆（去掉与x轴的交点），求出即可．
解答： 解：∵b=2，以AC为x轴，线段AB的垂直平分线为y轴，建立直角坐标系．
∴A（-1，0），C（1，0）．
∵a、b、c成等差数列，∴2b=a+c=4＞|AC|．
∴点B的轨迹是椭圆（去掉与x轴的交点），
设椭圆的标准方程为：
x2
m2
+
y2
n2
=1(m＞n＞0)．
则2m=2b=4，解得m=2，n2=22-12=3．
∴点B的轨迹方程为：
x2
4
+
y2
3
=1(x≠±2)．
点评：本题考查了椭圆的定义及其标准方程，属于基础题．
练习册系列答案
相关题目
一个几何体的三视图如图所示，其中俯视图为正三角形，则该几何体的外接球体积为（　　）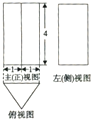
A、
64
3
π
9
B、
256
3
π
9
C、
64
3
π
27
D、
256
3
π
27
sin(
13π
4
)•cos(-
5π
3
)
tan(
23π
3
)
+
sin(-
21π
4
)
cos(
17π
6
)
化简的结果是（　　）
A、-
5
6
12
B、
6
4
C、-
6
4
D、
5
6
12
设椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的左焦点为F，离心率为
2
2
，椭圆与x轴左交点与点F的距离为
2
-1．
（Ⅰ）求椭圆方程；
（Ⅱ）过点P（0，2）的直线l与椭圆交于不同的两点A，B，当△OAB面积为
2
2
时，求|AB|．
已知数列{lgan}是等差数列，求证：数列{an}是等比数列．
已知函数f（x）=
-x2+
4
x
，x＞0
0，x=0
x2+
4
x
，x＜0
，若f（t）+f（t+2）＞0，则实数t的取值范围是（　　）
A、t＜-3-
3
或t＞-3+
3
B、t＞-1
C、t＜1-
3
或t＞1+
3
D、t＜-2
若函数f（x）=min{2x，x+2，10-x}（x≥0），则f（x）的最大值是
 
．
已知△ABC为等边三角形，AB=2，设点P，Q满足
AP
=λ
AB
，
AQ
=（1-λ）
AC
，λ∈R，若
BQ
•
CP
=-
5
2
，则λ=（　　）
A、
1
2
B、
1±
2
2
C、
1±
10
2
D、
-3±2
2
2
对于以下命题：
①|
a
|-|
b
|=|
a
+
b
|是
a
，
b
共线的充要条件；
②对空间任意一点O和不共线的三点A、B、C，若
OP
=2
OA
-
OB
+
OC
，则P、A、B、C四点共面．
③如果
a
•
b
＜0，那么
a
与
b
的夹角为钝角
④若{
a
，
b
，
c
}为空间一个基底，则{
a
+
b
，
b
+
c
，
c
+
a
}构成空间的另一个基底；
⑤若
m
=
a
-2
b
+3
c
，
n
=-2
a
+4
b
-6
c
，则
m
∥
n
．
其中不正确结论的序号是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网