题目内容
10．无论x取何值，多项式（m-1）x3+2mx2+（m+1）x+a都等于多项式ax2-bx+a，求（m+a）a-b的值．分析 利用多项式的表达式，求出m，a，b，然后求解表达式的值即可．
解答 解：无论x取何值，多项式（m-1）x3+2mx2+（m+1）x+a都等于多项式ax2-bx+a，
可得m-1=0，可得m=1，a=2m=2，b=-m-1=-2．
（m+a）a-b=34=81．
点评 本题考查多项式的应用，有理指数幂的运算，考查计算能力．
练习册系列答案
教材全解字词句篇系列答案
相关题目
20．已知f（x）=$\left\{\begin{array}{l}{ax^2+x，x＞0}\\{-2x，x≤0}\end{array}\right.$，若不等式f（x-2）≥f（x）对一切x∈R恒成立，则a的最小值为（ ）
| A． | -$\frac{7}{16}$ | B． | -$\frac{9}{16}$ | C． | -$\frac{1}{2}$ | D． | -$\frac{1}{4}$ |
7．运行如图所示的程序框图，则输出的S值为（ ）
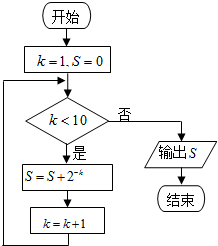
| A． | $\frac{{{2^9}-1}}{2^9}$ | B． | $\frac{{{2^9}+1}}{2^9}$ | C． | $\frac{{{2^{10}}-1}}{{{2^{10}}}}$ | D． | $\frac{{{2^{10}}}}{{{2^{10}}+1}}$ |