题目内容
（Ⅰ）如图1，A，B，C是平面内的三个点，且A与B不重合，P是平面内任意一点，若点C在直线AB上，试证明：存在实数λ，使得：
=λ
+(1-λ)
．
（Ⅱ）如图2，设G为△ABC的重心，PQ过G点且与AB、AC（或其延长线）分别交于P，Q点，若
=m
，
=n
，试探究：
+
的值是否为定值，若为定值，求出这个定值；若不是定值，请说明理由．
| PC |
| PA |
| PB |
（Ⅱ）如图2，设G为△ABC的重心，PQ过G点且与AB、AC（或其延长线）分别交于P，Q点，若
| AP |
| AB |
| AQ |
| AC |
| 1 |
| m |
| 1 |
| n |
分析：（I）由于A，B，C三点共线，所以存在实数λ使得：
=λ
，变形，可得结论；
（II）连结AG，利用G为△ABC的重心，结合（I）的结论即可得到结论．
| BC |
| BA |
（II）连结AG，利用G为△ABC的重心，结合（I）的结论即可得到结论．
解答：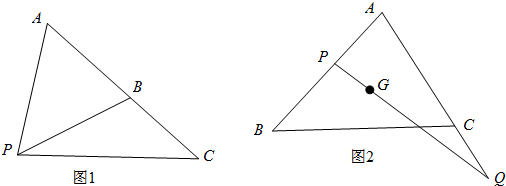
（Ⅰ）证明：由于A，B，C三点共线，所以存在实数λ使得：
=λ
，…（2分）
即
-
=λ(
-
)…（4分）
化简为
=λ
+(1-λ)
结论得证．…（6分）
（Ⅱ）解：连结AG，因为G为△ABC的重心，
所以：
=
•
(
+
)=
+
…（8分）
又因为
=m
，
=n
所以
=
+
=
+
…（10分）
由（Ⅰ）知：
+
=1所以
+
=3为定值．…（12分）
（Ⅰ）证明：由于A，B，C三点共线，所以存在实数λ使得：| BC |
| BA |
即
| PC |
| PB |
| PA |
| PB |
化简为
| PC |
| PA |
| PB |
结论得证．…（6分）
（Ⅱ）解：连结AG，因为G为△ABC的重心，
所以：
| AG |
| 2 |
| 3 |
| 1 |
| 2 |
| AB |
| AC |
| 1 |
| 3 |
| AB |
| 1 |
| 3 |
| AC |
又因为
| AP |
| AB |
| AQ |
| AC |
所以
| AG |
| 1 |
| 3 |
| AB |
| 1 |
| 3 |
| AC |
| 1 |
| 3m |
| AP |
| 1 |
| 3n |
| AQ |
由（Ⅰ）知：
| 1 |
| 3m |
| 1 |
| 3n |
| 1 |
| m |
| 1 |
| n |
点评：本题考查向量知识的运用，考查向量的共线，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
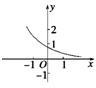14、函数f（x）=ax-b的图象如图，其中a、b为常数，则下列结论正确的是（ ）
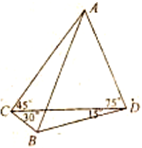某单位在抗雪救灾中，需要在A，B两地之间架设高压电线，测量人员在相距6km的C，D两地测得∠ACD=45°，∠ADC=75°，∠BDC=15°，∠BCD=30°（如图，其中A，B，C，D在同一平面上），假如考虑到电线的自然下垂和施工损耗等原因，实际所须电线长度大约应该是A，B之间距离的1.2倍，问施工单位至少应该准备多长的电线？
； 
，试探究：
的值是否为定值，若为定值，求出这个定值；若不是定值，请说明理由。 
．
，
，试探究：
的值是否为定值，若为定值，求出这个定值；若不是定值，请说明理由．