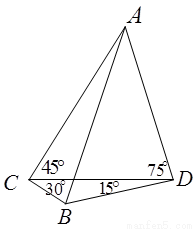题目内容
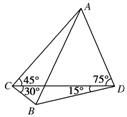
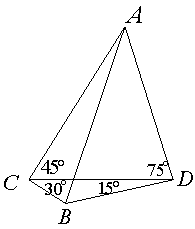
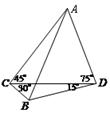
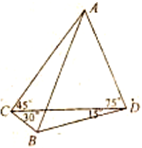 某单位在抗雪救灾中,需要在A,B两地之间架设高压电线,测量人员在相距6km的C,D两地测得∠ACD=45°,∠ADC=75°,∠BDC=15°,∠BCD=30°(如图,其中A,B,C,D在同一平面上),假如考虑到电线的自然下垂和施工损耗等原因,实际所须电线长度大约应该是A,B之间距离的1.2倍,问施工单位至少应该准备多长的电线?
某单位在抗雪救灾中,需要在A,B两地之间架设高压电线,测量人员在相距6km的C,D两地测得∠ACD=45°,∠ADC=75°,∠BDC=15°,∠BCD=30°(如图,其中A,B,C,D在同一平面上),假如考虑到电线的自然下垂和施工损耗等原因,实际所须电线长度大约应该是A,B之间距离的1.2倍,问施工单位至少应该准备多长的电线?分析:分别在△ACD、△BCD中,利用正弦定理,求出AD,BD,再在△ABD中,利用勾股定理,求AB,从而可求电线长度
解答:解:在△ACD中,∠ACD=45°,CD=6,∠ADC=75°,所以∠CAD=60°
∵
=
,∴AD=
=
=2
在△BCD中,∠BCD=30°,CD=6,∠BDC=15°,∴∠CBD=135°
∵
=
,∴BD=
=
=3
在△ABD中,∠BDA=∠BDC+∠ADC=90°,∴△ABD是直角三角形
∴AB=
=
∴电线长度至少为l=1.2×AB=
km
∵
| CD |
| sin∠CAD |
| AD |
| sin∠ACD |
| CD×sin∠ACD |
| sin∠CAD |
6×
| ||||
|
| 6 |
在△BCD中,∠BCD=30°,CD=6,∠BDC=15°,∴∠CBD=135°
∵
| CD |
| sin∠CBD |
| BD |
| sin∠BCD |
| CD×sin∠BCD |
| sin∠CBD |
6×
| ||||
|
| 2 |
在△ABD中,∠BDA=∠BDC+∠ADC=90°,∴△ABD是直角三角形
∴AB=
| AD2+BD2 |
| 42 |
∴电线长度至少为l=1.2×AB=
| 6 |
| 5 |
| 42 |
点评:本题利用正弦定理解决实际问题,解题的关键是确定三角形,正确运用正弦定理,属于中档题.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
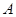 、
、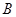 两地之间架设高压电线,测量人员在相距
两地之间架设高压电线,测量人员在相距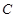 、
、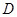 两地(
两地(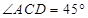 ,
,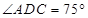 ,
,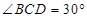 ,
,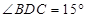 (如图),假如考虑到电线的自然下垂和施工损耗等原因,实际所须电线长度大约应该是
(如图),假如考虑到电线的自然下垂和施工损耗等原因,实际所须电线长度大约应该是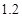 倍,问施工单
倍,问施工单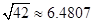 )
)