Question

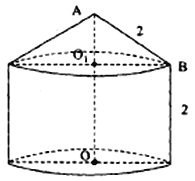
【题目】某粮库拟建一个储粮仓如图所示，其下部是高为2的圆柱，上部是母线长为2的圆锥，现要设计其底面半径和上部圆锥的高，若设圆锥的高为，储粮仓的体积为.

（1）求关于的函数关系式；（圆周率用表示）

（2）求为何值时，储粮仓的体积最大.

Answer 1

【答案】（Ⅰ）， .（Ⅱ）.

【解析】试题分析：（Ⅰ）由题圆锥和圆柱的底面半径， 可得储粮仓的体积， .

（Ⅱ）利用导数求（Ⅰ）中的函数最值即可.

试题解析：（Ⅰ）∵圆锥和圆柱的底面半径， ∴.

∴，即， .

（Ⅱ），令 ，

解得， .又，∴（舍去）.

当变化时， 的变化情况如下表：

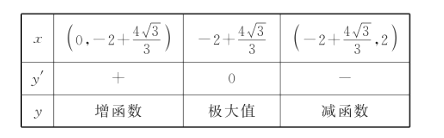
故当时，储粮仓的体积最大.

点晴：研究数学模型，建立数学模型，进而借鉴数学模型，对提高解决实际问题的能力，以及提高数学素养都是十分重要的．建立模型的步骤可分为： (1) 分析问题中哪些是变量，哪些是常量，分别用字母表示； (2) 根据所给条件，运用数学知识，确定等量关系； (3) 写出f(x)的解析式并指明定义域.