题目内容
19.已知函数f(x)满足f(x+1)=f(x-1),且f(x)是偶函数,当x∈[0,1]时,f(x)=2x-1,若在区间[-1,3]内,函数g(x)=f(x)-kx-k有4个零点,则实数k的取值范围是( )| A. | $[\frac{1}{4},\frac{1}{3})$ | B. | $(0,\frac{1}{2})$ | C. | $(0,\frac{1}{4}]$ | D. | $(\frac{1}{3},\frac{1}{2})$ |
分析 函数g(x)=f(x)-kx-k有4个零点可化为函数f(x)与y=kx+k在[-1,3]内的图象有四个不同的交点,从而作图求得.
解答 解:∵f(x+1)=f(x-1),
∴函数f(x)的周期为2,
∴作函数f(x)与y=kx+k在[-1,3]内的图象如下, ,
,
直线y=kx+k过点(-1,0);
当过点(3,1)时,直线的斜率k=$\frac{1-0}{3-(-1)}$=$\frac{1}{4}$,
故结合图象可知,
0<k≤$\frac{1}{4}$;
故选C.
点评 本题考查了函数的性质的判断与应用,同时考查了数形结合的思想应用.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
14.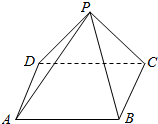 已知正四面棱锥P-ABCD的侧棱长为2$\sqrt{3}$,侧面等腰三角形的顶角为30°,则从A点出发环绕面一周后回到A点的最短路程为( )
已知正四面棱锥P-ABCD的侧棱长为2$\sqrt{3}$,侧面等腰三角形的顶角为30°,则从A点出发环绕面一周后回到A点的最短路程为( )
 已知正四面棱锥P-ABCD的侧棱长为2$\sqrt{3}$,侧面等腰三角形的顶角为30°,则从A点出发环绕面一周后回到A点的最短路程为( )
已知正四面棱锥P-ABCD的侧棱长为2$\sqrt{3}$,侧面等腰三角形的顶角为30°,则从A点出发环绕面一周后回到A点的最短路程为( )| A. | 2$\sqrt{6}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{6}$ | D. | 6 |
11.把函数y=ex的图象按向量$\overrightarrow{a}$=(2,0)平移,得到y=f(x)的图象,则f(x)=( )
| A. | ex+2 | B. | ex-2 | C. | ex+2 | D. | ex-2 |