题目内容
(本小题满分14分)已知函数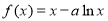 ,
, ,
, ;
;
(1)设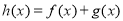 ,若
,若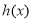 在定义域内存在极值,求
在定义域内存在极值,求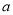 的取值范围;
的取值范围;
(2)设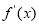 是
是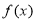 的导函数,若
的导函数,若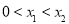 ,
,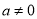 ,
,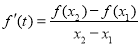
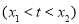 ,求证:
,求证: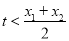 .
.
(1)a>2;(2)见解析
【解析】
试题解析:(1) h(x)定义域为(0,+∞).
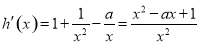 2分
2分
令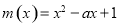 ,其判别式
,其判别式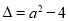 .
.
①当|a|≤2时,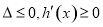 ,h(x)在(0,+∞)上单调递增.无极值点.
,h(x)在(0,+∞)上单调递增.无极值点.
②当a <-2时,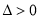 ,m(x)=0的两根都小于0 ,在(0,+∞)上,h′(x)>0,
,m(x)=0的两根都小于0 ,在(0,+∞)上,h′(x)>0,
故h(x)在(0,+∞)上单调递增.无极值点.
③当a>2时, Δ>0,m(x)=0的两根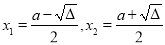 ,
,
当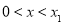 时,h′(x)>0,当
时,h′(x)>0,当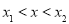 时,h′(x)<0,
时,h′(x)<0,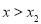 时,h′(x)>0 5分
时,h′(x)>0 5分
故h(x)分别在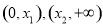 上单调递增,在
上单调递增,在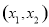 上单调递减.所以存在两个极值点,
上单调递减.所以存在两个极值点,
所以a>2 . 6分
另解: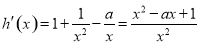 , 1分
, 1分
要使h(x)在定义域 (0,+∞)存在极值,即方程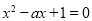 在(0,+∞)有2个根,
在(0,+∞)有2个根,
令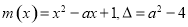 ,则方程
,则方程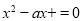 在(0,+∞)有2个根等价于
在(0,+∞)有2个根等价于
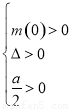 4 分
4 分
 ,所以存在两个极值点.
,所以存在两个极值点.
所以a>2. 6 分
(2)由(1)知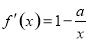 ,所以
,所以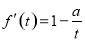 ,
,
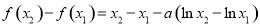 ,
,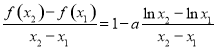 ,
,
由 ,
,
所以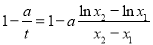 ?,即
?,即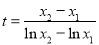 8 分
8 分
所以要证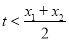 ,只要证
,只要证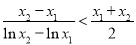 ,
,
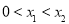 ,只要证
,只要证 ,只要证
,只要证 10分
10分
令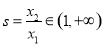 ,只要证2(s-1)<(1+s)lns,s>1.
,只要证2(s-1)<(1+s)lns,s>1.
设r(s)=(1+s)lns-2(s-1), 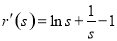 ,
, ,
,
所以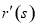 在(1,+
在(1,+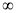 )上为增函数,
)上为增函数, ,所以
,所以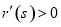 ,所以r(s)在(1,+
,所以r(s)在(1,+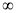 )递增,r(1)=0,
)递增,r(1)=0,
所以r(s)>0,即(1+s)lns-2(s-1)>0,结论得证.
考点:考查利用导数研究函数的极值,导数与不等式的综合应用.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 (其中
(其中 ),若
),若 ,则
,则 在同一坐标系内的大致图象是
在同一坐标系内的大致图象是
 在点
在点 处的切线与直线
处的切线与直线 垂直,则
垂直,则 ————.
————. 的值为( )
的值为( )
 B.
B. C.
C. D.
D.
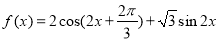
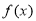 的最小正周期和最大值;
的最小正周期和最大值; 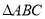 的三内角分别是A、B、C.若
的三内角分别是A、B、C.若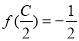 ,且
,且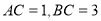 ,求
,求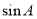 的值.
的值. 满足
满足 ,
, ,且前
,且前 项之和等于
项之和等于 ,则该数列的通项公式
,则该数列的通项公式 .
. 的各项均为正数,且
的各项均为正数,且 ,则
,则 .
. 上是增函数,则实数
上是增函数,则实数 的取值范围是__________.
的取值范围是__________.