题目内容
【题目】椭圆![]() (
(![]() ),原点
),原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,其中:点
,其中:点![]() ,点
,点![]() .
.
(1)求该椭圆![]() 的离心率
的离心率![]() ;
;
(2)经过椭圆右焦点![]() 的直线
的直线![]() 和该椭圆交于
和该椭圆交于![]() 两点,点
两点,点![]() 在椭圆上,
在椭圆上, ![]() 为原点,若
为原点,若![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】试题分析:(Ⅰ)求椭圆离心率,只需建立一个等量关系,解出![]() :利用点到直线距离公式可得
:利用点到直线距离公式可得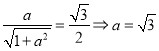 ,而
,而![]() ,所以
,所以![]() ,离心率
,离心率![]() (Ⅱ)设
(Ⅱ)设![]()
![]()
![]() ,先用坐标表示
,先用坐标表示![]() ,
, ![]() ,因此
,因此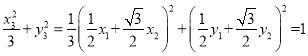 ,化简得
,化简得![]() ,这样就转化为直线与椭圆位置关系问题:联立直线方程与椭圆方程,消去一个未知数得另一未知数的方程,结合韦达定理得两根之积,代入可解得直线斜率,即直线方程
,这样就转化为直线与椭圆位置关系问题:联立直线方程与椭圆方程,消去一个未知数得另一未知数的方程,结合韦达定理得两根之积,代入可解得直线斜率,即直线方程
试题解析:(Ⅰ)设直线![]() :
: ![]() 且
且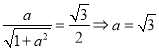
所以离心率![]() .
.
(Ⅱ)椭圆![]() 方程为
方程为![]() ,设
,设![]()
![]()
![]()
①当直线斜率为0时,其方程为![]() ,
,
此时![]() ,
, ![]() ,不满足
,不满足![]() ,不符合题意,舍去
,不符合题意,舍去
②当直线斜率不为0时设直线方程为![]() ,
,
由题: 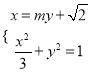 消
消![]() 得
得![]() ,
,
所以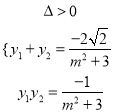
因为![]() ,所以
,所以![]() ,
, ![]()
因为点![]() 在椭圆上,
在椭圆上,
所以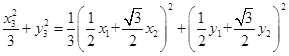
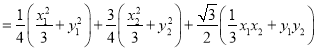
![]()
所以![]()
![]()
![]()
![]()
化简得![]() ,得
,得![]() 直线为
直线为![]()
综上,直线为![]()

练习册系列答案
相关题目
【题目】某数学教师对所任教的两个班级各抽取20名学生进行测试,分数分布如表:
分数区间 | 甲班频率 | 乙班频率 |
| 0.1 | 0.2 |
| 0.2 | 0.2 |
| 0.3 | 0.3 |
| 0.2 | 0.2 |
| 0.2 | 0.1 |
(Ⅰ)若成绩120分以上(含120分)为优秀,求从乙班参加测试的90分以上(含90分)的同学中,随机任取2名同学,恰有1人为优秀的概率;
(Ⅱ)根据以上数据完成下面的![]() ×
×![]() 列联表:
列联表:
优秀 | 不优秀 | 总计 | |
甲班 | |||
乙班 | |||
总计 |
在犯错概率小于0.1的前提下,你是否有足够的把握认为学生的数学成绩是否优秀与班级有关系?
参考公式: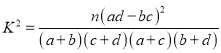 ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|