题目内容
设短轴长为是2| 3 |
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| a2 |
分析:根据题意椭圆与双曲线的离心率互为倒数可得椭圆的方程为
+
=1,设出直线方程联立椭圆方程得到一元二次方程,由△=0可得关于k的方程,再结合直线l1,l2互相垂直且两条直线与椭圆的交点只有一个得到x0y0的关系即得到圆的方程,最后检验斜率不存在时也符合题意即可.
| x2 |
| 6 |
| y2 |
| 3 |
解答:解: 双曲线
双曲线
-
=1的离心率为
,于是椭圆C:
+
=1(a>b>0)的离心率为
.
即a=
c,又由题意,2b=2
以及b2+c2=a2,解得a=
, b=c=
,
椭圆C的方程为
+
=1.
设P(x0,y0)是⊙E上的任意一点,过P的直线l:y=k(x-x0)+y0,
代入
+
=1中,得
+
=1,
即(1+2k2)x2+4k(y0-kx0)x+2(y0-kx0)2-6=0,①
若直线l与椭圆的公共点只有一个,则①中判别式△=0,
即16k2(y0-kx0)2-8(1+2k2)[(y0-kx0)2-3]=0,
整理得关于k的方程:(6-x02)k2+2x0y0k-y02+3=0,②
要使得⊙E上面的每一个点都可以作两条互相垂直的直线l1,l2,
且l1,l2与椭圆的公共点都只有一个,方程必须有两根且两根之积为-1,故
=-1,即x02+y02=9,
又对于点(
,
),(-
,
),(
, -
),(-
, -
),直线l1,l2中有一条斜率不存在,
另一条斜率为0,显然成立.故这样的⊙E,方程为:x2+y2=9.
故答案为x2+y2=9.
 双曲线
双曲线| x2 |
| a2 |
| y2 |
| a2 |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
即a=
| 2 |
| 3 |
| 6 |
| 3 |
椭圆C的方程为
| x2 |
| 6 |
| y2 |
| 3 |
设P(x0,y0)是⊙E上的任意一点,过P的直线l:y=k(x-x0)+y0,
代入
| x2 |
| 6 |
| y2 |
| 3 |
| x2 |
| 6 |
| (kx-kx0+y0)2 |
| 3 |
即(1+2k2)x2+4k(y0-kx0)x+2(y0-kx0)2-6=0,①
若直线l与椭圆的公共点只有一个,则①中判别式△=0,
即16k2(y0-kx0)2-8(1+2k2)[(y0-kx0)2-3]=0,
整理得关于k的方程:(6-x02)k2+2x0y0k-y02+3=0,②
要使得⊙E上面的每一个点都可以作两条互相垂直的直线l1,l2,
且l1,l2与椭圆的公共点都只有一个,方程必须有两根且两根之积为-1,故
| -y02+3 |
| 6-x02 |
又对于点(
| 6 |
| 3 |
| 6 |
| 3 |
| 6 |
| 3 |
| 6 |
| 3 |
另一条斜率为0,显然成立.故这样的⊙E,方程为:x2+y2=9.
故答案为x2+y2=9.
点评:截距处理问题的关键是进行准确的运算,抓住题目的关键如垂直关系、只有一个交点,直线与圆锥曲线的综合性问题,多为把关题,是学生的学习难点也是高考的重点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
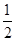 ,短轴长为4
,短轴长为4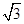 .
.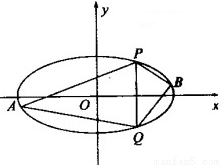
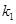 ,直线PB的斜率为
,直线PB的斜率为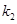 ,判断
,判断 m米的椭圆上 .
m米的椭圆上 .