题目内容
已知平面向量 ,
, 满足|
满足| |=3,|
|=3,| |=2,
|=2, 与
与 的夹角为60°,若(
的夹角为60°,若( -m
-m )⊥
)⊥ ,则实数m=________.
,则实数m=________.
3
分析:由题意可得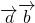 =3×2×cos60°=3,(
=3×2×cos60°=3,(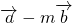 )•
)• =
= -m
-m =9-m×3=0,解方程求得实数m的值.
=9-m×3=0,解方程求得实数m的值.
解答:由题意可得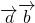 =3×2×cos60°=3,(
=3×2×cos60°=3,(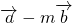 )•
)• =
= -m
-m =9-m×3=0,
=9-m×3=0,
∴m=3,
故答案为:3.
点评:本题考查两个向量的数量积的定义,数量积公式的应用,两个向量垂直的性质,求出 =3,是解题的关键.
=3,是解题的关键.
分析:由题意可得
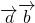 =3×2×cos60°=3,(
=3×2×cos60°=3,(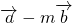 )•
)• =
= -m
-m =9-m×3=0,解方程求得实数m的值.
=9-m×3=0,解方程求得实数m的值.解答:由题意可得
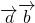 =3×2×cos60°=3,(
=3×2×cos60°=3,(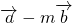 )•
)• =
= -m
-m =9-m×3=0,
=9-m×3=0,∴m=3,
故答案为:3.
点评:本题考查两个向量的数量积的定义,数量积公式的应用,两个向量垂直的性质,求出
 =3,是解题的关键.
=3,是解题的关键. 
练习册系列答案
相关题目
 ,
, 满足:
满足: ,则
,则 的夹角为
的夹角为  ,且α与
,且α与 的夹角为
的夹角为 ,则
,则 的取值范围是
;
的取值范围是
; ,满足
,满足 。若
。若
 有最大值
有最大值 B.
B. D.
D.