题目内容
P点在椭圆 +
+ =1上运动,Q,R分别在两圆(x+1)2+y2=1和(x-1)2+y2=1上运动,则|PQ|+|PR|的最大值为 .
=1上运动,Q,R分别在两圆(x+1)2+y2=1和(x-1)2+y2=1上运动,则|PQ|+|PR|的最大值为 .
【答案】分析:确定椭圆焦点F1(-1,0),F2(1,0)恰为两圆(x+1)2+y2=1和(x-1)2+y2=1的圆心,利用椭圆的定义,即可得出结论.
解答: 解:∵椭圆
解:∵椭圆 +
+ =1中,c2=4-3=1,
=1中,c2=4-3=1,
∴椭圆 +
+ =1两焦点F1(-1,0),F2(1,0)恰为两圆(x+1)2+y2=1和(x-1)2+y2=1的圆心,
=1两焦点F1(-1,0),F2(1,0)恰为两圆(x+1)2+y2=1和(x-1)2+y2=1的圆心,
 ,准线x=±
,准线x=± =±4,
=±4,
过P点作x轴平行线,分别交两准线于A,B两点,
连接PF1,PF2,并延长,分别交两圆于Q′,R′,
则|PQ|+|PR|≤|PQ′|+|PR′|=|PF1|+1+|PF2|+1=e|PA|+e|PB|+2=e|AB|+2
= =6.
=6.
故答案为:6
点评:本题考查椭圆和圆的简单性质,考查学生分析解决问题的能力,属于中档题.
解答:
 解:∵椭圆
解:∵椭圆 +
+ =1中,c2=4-3=1,
=1中,c2=4-3=1,∴椭圆
 +
+ =1两焦点F1(-1,0),F2(1,0)恰为两圆(x+1)2+y2=1和(x-1)2+y2=1的圆心,
=1两焦点F1(-1,0),F2(1,0)恰为两圆(x+1)2+y2=1和(x-1)2+y2=1的圆心, ,准线x=±
,准线x=± =±4,
=±4,过P点作x轴平行线,分别交两准线于A,B两点,
连接PF1,PF2,并延长,分别交两圆于Q′,R′,
则|PQ|+|PR|≤|PQ′|+|PR′|=|PF1|+1+|PF2|+1=e|PA|+e|PB|+2=e|AB|+2
=
 =6.
=6.故答案为:6
点评:本题考查椭圆和圆的简单性质,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
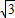 的直线l过点(0,-2
的直线l过点(0,-2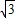 )和椭圆C:
)和椭圆C: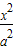 +
+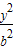 =1 (a>b>0)的焦点,且椭圆C的中心关于直线l的对称点在椭圆C的右准线上.
=1 (a>b>0)的焦点,且椭圆C的中心关于直线l的对称点在椭圆C的右准线上.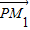 =λ
=λ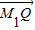 ,
,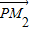 =μ
=μ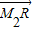 ,当P点在椭圆C上运动时,试问λ+μ是否为定值,并请说明理由.
,当P点在椭圆C上运动时,试问λ+μ是否为定值,并请说明理由.