题目内容
已知斜率为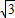 的直线l过点(0,-2
的直线l过点(0,-2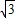 )和椭圆C:
)和椭圆C: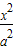 +
+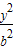 =1 (a>b>0)的焦点,且椭圆C的中心关于直线l的对称点在椭圆C的右准线上.
=1 (a>b>0)的焦点,且椭圆C的中心关于直线l的对称点在椭圆C的右准线上.(1)求椭圆C的方程;
(2)点P,Q,R都在椭圆C上,PQ、PR分别过点M1(-1,0)、M2(1,0),设
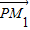 =λ
=λ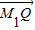 ,
,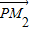 =μ
=μ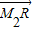 ,当P点在椭圆C上运动时,试问λ+μ是否为定值,并请说明理由.
,当P点在椭圆C上运动时,试问λ+μ是否为定值,并请说明理由.
【答案】分析:(1)利用点斜式即可得出直线l的方程,令y=0即可得出椭圆的焦点(c),利用轴对称的性质即可得出原点关于l的对称点,利用准线方程x=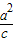 即可得出a,再利用b2=a2-c2即可;
即可得出a,再利用b2=a2-c2即可;
(2)设P(x,y),Q(x1,y1),R(x2,y2),
i)当x=x1=-1时,ii)当x=x2=-1时,容易得出λ+μ的值为定值;
iii)当x≠x1且x≠x2时,利用向量运算及相等可得x1,y1与x,y及λ的关系,同理得到x2,y2与x,y及μ的关系,再代入椭圆的方程即可得出.
解答:解:(1)由题意可得直线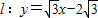 ,令y=0,解得x=2,∴c=2.
,令y=0,解得x=2,∴c=2.
∴椭圆的焦点为(±2,0),
设原点关于l的对称点为(x,y),
则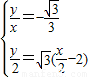 ,解得x=3,即
,解得x=3,即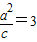 ,a2=6,∴b2=a2-c2=2.
,a2=6,∴b2=a2-c2=2.
∴椭圆的方程为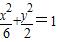 .
.
(2)设P(x,y),Q(x1,y1),R(x2,y2),
i)当x=x1=-1时,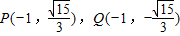 ,
,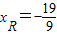 ,
,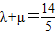
ii)同理当x=x2=-1时,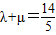
iii)当x≠x1且x≠x2时,
由题意得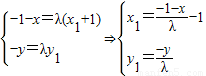
代入椭圆方程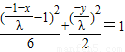 ,即
,即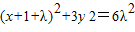 ,
,
又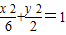 ,有
,有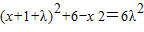 ,
,
即5λ2-(2x+2)λ+2x+7=0(5λ-2x-7)(λ-1)=0,
同理可得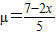 ,
,
∴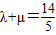 .
.
点评:熟练掌握椭圆的标准方程及其性质、轴对称的性质、点在椭圆上转化为点的坐标适合题意的方程、向量的运算与相等等是解题的关键.
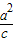 即可得出a,再利用b2=a2-c2即可;
即可得出a,再利用b2=a2-c2即可;(2)设P(x,y),Q(x1,y1),R(x2,y2),
i)当x=x1=-1时,ii)当x=x2=-1时,容易得出λ+μ的值为定值;
iii)当x≠x1且x≠x2时,利用向量运算及相等可得x1,y1与x,y及λ的关系,同理得到x2,y2与x,y及μ的关系,再代入椭圆的方程即可得出.
解答:解:(1)由题意可得直线
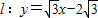 ,令y=0,解得x=2,∴c=2.
,令y=0,解得x=2,∴c=2.∴椭圆的焦点为(±2,0),
设原点关于l的对称点为(x,y),
则
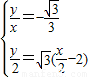 ,解得x=3,即
,解得x=3,即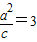 ,a2=6,∴b2=a2-c2=2.
,a2=6,∴b2=a2-c2=2.∴椭圆的方程为
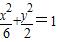 .
.(2)设P(x,y),Q(x1,y1),R(x2,y2),
i)当x=x1=-1时,
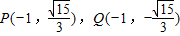 ,
,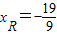 ,
,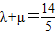
ii)同理当x=x2=-1时,
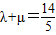
iii)当x≠x1且x≠x2时,
由题意得
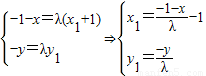
代入椭圆方程
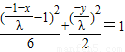 ,即
,即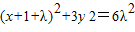 ,
,又
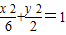 ,有
,有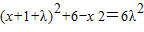 ,
,即5λ2-(2x+2)λ+2x+7=0(5λ-2x-7)(λ-1)=0,

同理可得
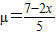 ,
,∴
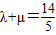 .
.点评:熟练掌握椭圆的标准方程及其性质、轴对称的性质、点在椭圆上转化为点的坐标适合题意的方程、向量的运算与相等等是解题的关键.

练习册系列答案
相关题目
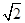 倍后得到点Q(x,
倍后得到点Q(x,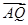 ·
· =1.
=1.  的直线L交曲线C于M、N两点,且
的直线L交曲线C于M、N两点,且 +
+ +
+ =
=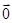 ,试求△MNH的面积.
,试求△MNH的面积. 倍后得到点Q(x,
倍后得到点Q(x, ·
· =1.
=1. 的直线l交曲线C于M、N两点,且
的直线l交曲线C于M、N两点,且 +
+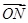 +
+ =
= ,试求△MNH的面积.
,试求△MNH的面积.