题目内容
已知P点在椭圆
解:∵P点在椭圆![]() =1上,
=1上,
∴可设P点的坐标为(5cosθ,4sinθ),
即x=5cosθ,y=4sinθ.
∴z=4x-5y+6
=4×5cosθ-5×4sinθ+6
=-20![]() ·(
·(![]() sinθ-
sinθ-![]() cosθ)+6
cosθ)+6
=-20![]() sin(θ-
sin(θ-![]() )+6.∴当θ=2kπ-
)+6.∴当θ=2kπ-![]() (k∈Z)时,z最大,其最大值为6+20
(k∈Z)时,z最大,其最大值为6+20![]() ;
;
当θ=2kπ+![]() (k∈Z)时,z最小,其最小值为6-20
(k∈Z)时,z最小,其最小值为6-20![]() .
.
点评:利用椭圆的参数方程,把z=4x-5y+6转化成θ的三角函数是解决本例的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
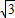 的直线l过点(0,-2
的直线l过点(0,-2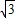 )和椭圆C:
)和椭圆C: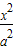 +
+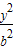 =1 (a>b>0)的焦点,且椭圆C的中心关于直线l的对称点在椭圆C的右准线上.
=1 (a>b>0)的焦点,且椭圆C的中心关于直线l的对称点在椭圆C的右准线上.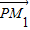 =λ
=λ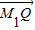 ,
,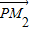 =μ
=μ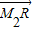 ,当P点在椭圆C上运动时,试问λ+μ是否为定值,并请说明理由.
,当P点在椭圆C上运动时,试问λ+μ是否为定值,并请说明理由.