题目内容
 如图,过抛物线y2=8x的焦点F的直线交抛物线与圆(x-2)2+y2=4于A,B,C,D四点,则|AB|•|CD|=________.
如图,过抛物线y2=8x的焦点F的直线交抛物线与圆(x-2)2+y2=4于A,B,C,D四点,则|AB|•|CD|=________.
4
分析:由题设条件知,圆心即抛物线的焦点,结合图形可得出|AB|=|AF|-|BF|=xA,|CD|=|DF|-|CF|=xD,即|AB|•|CD|=xA×xD,再分直线AB的斜率存在与不存在两种情况讨论即可得出答案
解答:由题意,抛物线y2=8x的焦点F(2,0),圆(x-2)2+y2=4圆心为(2,0),即圆心为焦点
∴|AB|=|AF|-|BF|=xA,|CD|=|DF|-|CF|=xD
若直线AD与X轴垂直,此时xA=xD=2,故有|AB|•|CD|=xA×xD=4
若直线AD与X轴不垂直,此时斜率存在,可设为k,则有lAD:y=k(x-2)
代入抛物线y2=8x整理得k2x2-4(k2+2)+4k2=0
由根与系数的关系得xA×xD=4
综上知xA×xD=4,即|AB|•|CD|=4
故答案为4
点评:本题考查直线与圆锥曲线的综合问题,抛物线的性质及圆的标准方程,解题的关键是将求|AB|•|CD|的值转化为求xA×xD的值
分析:由题设条件知,圆心即抛物线的焦点,结合图形可得出|AB|=|AF|-|BF|=xA,|CD|=|DF|-|CF|=xD,即|AB|•|CD|=xA×xD,再分直线AB的斜率存在与不存在两种情况讨论即可得出答案
解答:由题意,抛物线y2=8x的焦点F(2,0),圆(x-2)2+y2=4圆心为(2,0),即圆心为焦点
∴|AB|=|AF|-|BF|=xA,|CD|=|DF|-|CF|=xD
若直线AD与X轴垂直,此时xA=xD=2,故有|AB|•|CD|=xA×xD=4
若直线AD与X轴不垂直,此时斜率存在,可设为k,则有lAD:y=k(x-2)
代入抛物线y2=8x整理得k2x2-4(k2+2)+4k2=0
由根与系数的关系得xA×xD=4
综上知xA×xD=4,即|AB|•|CD|=4
故答案为4
点评:本题考查直线与圆锥曲线的综合问题,抛物线的性质及圆的标准方程,解题的关键是将求|AB|•|CD|的值转化为求xA×xD的值

练习册系列答案
相关题目
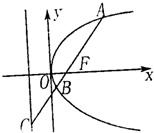 如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为
如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为 78、如图,过抛物线y2=4x的焦点F的直线交抛物线与圆(x-1)2+y2=1于A,B,C,D四点,则|AB|•|CD|=
78、如图,过抛物线y2=4x的焦点F的直线交抛物线与圆(x-1)2+y2=1于A,B,C,D四点,则|AB|•|CD|= 如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A、B(|AF|>|BF|),交其准线于点C,若|BC|=2|BF|,且|AF|=2,则此抛物线的方程为
如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A、B(|AF|>|BF|),交其准线于点C,若|BC|=2|BF|,且|AF|=2,则此抛物线的方程为 如图,过抛物线y2=2px(p>0)的焦点F且倾斜角为60°的直线l交抛物线于A、B两点,若|AF|=3,则此抛物线方程为( )
如图,过抛物线y2=2px(p>0)的焦点F且倾斜角为60°的直线l交抛物线于A、B两点,若|AF|=3,则此抛物线方程为( ) 如图,过抛物线y2=4x焦点的直线依次交抛物线与圆(x-1)2+y2=1于A,B,C,D,则
如图,过抛物线y2=4x焦点的直线依次交抛物线与圆(x-1)2+y2=1于A,B,C,D,则