题目内容

已知椭圆C:+=1.

(1)直线y=x+m与椭圆C有两个公共点,求实数m的范围;

(2)以椭圆C的焦点F1、F2为焦点,经过直线x+y=9上一点P作椭圆C1,当C1的长轴最短时,求C1的方程.

 

思路分析:椭圆及标准方程与代数、三角等内容常常横向综合.在解题时,应根据椭圆的特征,运用转化的思想,把曲线与方程和函数联系起来.

解:(1)直线y=x+m与椭圆C有两个公共点的条件是方程组有两组不同的解,

消去y得3x2+4mx+2m2-8=0.

∴Δ=16m2-12(2m2-8)＞0.

∴-2＜m＜2.

(2)依题意F1(-2,0)、F2(2,0),过F1作关于直线x+y=9的对称点F1′(9,11),设P是直线x+y=9与椭圆C的公共点.

∴2a=|PF1|+|PF2|=|PF1′|+|PF2|≥|F1′F2|=.

∴(2a)min=.

此时a2=,b2=a2-c2=.

故所求椭圆方程为=1.


练习册系列答案
相关题目
已知椭圆C 1：
x2
a2
+
y2
b2
=λ1（a＞b＞0，λ1＞0）和双曲线C 2：
x2
m2
-
y2
n2
=λ2(λ2≠0)，给出下列命题：
①对于任意的正实数λ1，曲线C1都有相同的焦点；
②对于任意的正实数λ1，曲线C1都有相同的离心率；
③对于任意的非零实数λ2，曲线C2都有相同的渐近线；
④对于任意的非零实数λ2，曲线C2都有相同的离心率．
其中正确的为（　　）

（07年陕西卷） (14分)

已知椭圆C:=1(a＞b＞0)的离心率为,短轴一个端点到右焦点的距离为.

(Ⅰ)求椭圆C的方程;

(Ⅱ)设直线l与椭圆C交于A、B两点，坐标原点O到直线l的距离为，求△AOB面积的最大值.

已知椭圆C:=1()的离心率为,短轴一个端点到右焦点的距离为.

(1)求椭圆的方程；

(2)设直线与椭圆交于、两点，坐标原点到直线的距离为，求△面积的最大值.

已知椭圆C:+=1(a>b>0)的一个顶点为A(2,0),离心率为.直线y=k(x-1)与椭圆C交于不同的两点M,N.

(1)求椭圆C的方程;

(2)当△AMN的面积为时,求k的值.

 

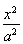
（本小题满分12分）

       已知椭圆C: +=1（a＞b＞0）的离心率e=，且椭圆经过点N（2，-3）．

   （1）求椭圆C的方程；

   （2）求椭圆以M（-1，2）为中点的弦所在直线的方程．

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网