Question

4．现有两个一元二次函数f（x），g（x）及实数t（t＞0）满足以下条件：
①f（x）+g（x）=x²+16x+13；②g（t）=25；③当x=t时，f（x）有最大值5；④g（x）的最小值为-2．
（1）求g（x）的解析式和t的值；
（2）设h（x）=|g（x）-10|，求h（x）在区间[a-4，a]上的最大值．

Answer 1

分析 （1）结合已知可得f（t）+g（t）=25+5，进而可得t值，设f（x）=a（x-1）²+5，（a＜0），则g（x）=（1-a）x²+（2a+16）x+8-a，（a＜0），由g（x）的最小值为-2，可得g（x）的解析式；
（2）画出函数h（x）的图象，分类讨论不同情况下h（x）在区间[a-4，a]上的最大值，可得答案．

解答 解：（1）由①f（x）+g（x）=x²+16x+13；②g（t）=25；③当x=t时，f（x）有最大值5，
故f（t）+g（t）=t²+16t+13=25+5，t＞0，
解得：t=1，或t=-17（舍去）；
则f（x）=a（x-1）²+5=ax²-2ax+a+5，（a＜0），
∴g（x）=（1-a）x²+（2a+16）x+8-a，（a＜0），
由g（x）的最小值为-2得：$\frac{4（1-a）（8-a）-（2a+16）^{2}}{4（1-a）}$=-2，
解得：a=-2，
∴g（x）=3x²+12x+10；
（2）∵h（x）=|g（x）-10|=|3x²+12x|=$\left\{\begin{array}{l}3{x}^{2}+12x，x＜-4，或x＞0\\-3{x}^{2}-12x，-4≤x≤0\end{array}\right.$，
故函数h（x）的图象如下图所示：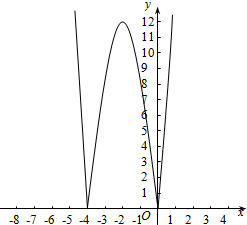

令h（x）=h（-2）=12，则x=-2，或x=-2-$2\sqrt{2}$，或x=-2+$2\sqrt{2}$，
当a-4＜-2-$2\sqrt{2}$，即a＜2-$2\sqrt{2}$时，h（x）在区间[a-4，a]上的最大值为h（a-4）=3a²-12a
当a-4≥-2-$2\sqrt{2}$，且a≤-2+$2\sqrt{2}$，即2-$2\sqrt{2}$≤a≤-2+$2\sqrt{2}$时，h（x）在区间[a-4，a]上的最大值为h（-2）=12；
当a＞-2+$2\sqrt{2}$，h（x）在区间[a-4，a]上的最大值为h（a）=3a²+12a，

点评 本题考查的知识点是二次函数的图象和性质，熟练掌握二次函数的图象和性质，是解答的关键．