题目内容
若函数f(x)的导函数是
(x)=－x(x+1)，则函数g(x)=f(logax)(0＜a＜1)的单调递减区间是（ ）
(x)=－x(x+1)，则函数g(x)=f(logax)(0＜a＜1)的单调递减区间是（ ）| A．[－1,0] | B．[ ，+∞),(0,1] |
| C．[1, ] | D．(－∞,) ，(,+∞) |
C
由(x)=－x(x+1)知,－1＜x＜0时, (x)＞0
f(x)是增函数;
x＞0或x＜－1时,(x)＜0f(x)是减函数;
而0＜a＜1时,logax为减函数
所以由复合函数的性质知, 若函数g(x)=f(logax)(0＜a＜1)为单调递减函数,则－1＜logax＜0x∈[1, ]
(x)=－x(x+1)知,－1＜x＜0时, (x)＞0f(x)是增函数;x＞0或x＜－1时,
(x)＜0f(x)是减函数;而0＜a＜1时,logax为减函数
所以由复合函数的性质知, 若函数g(x)=f(logax)(0＜a＜1)为单调递减函数,则－1＜logax＜0
x∈[1, ]
练习册系列答案
阅读快车系列答案
相关题目
.
为常数且
时，求
；
满足
，但
，则称
的二阶周期点.证明函数
；
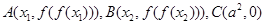，记
的面积为
，求
上的最大值和最小值。
残骸,我国“雪龙号”科考船于2014年3月26日从港口
出发，沿北偏东
角的射线
方向航行，而在港口北偏东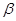
角的方向上有一个给科考船补给物资的小岛
，
海里，且
.现指挥部需要紧急征调位于港口
海里的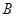
处的补给船，速往小岛
方向全速追赶科考船，并在
处相遇．经测算当两船运行的航线与海岸线
围成的三角形
的面积
最小时，这种补给方案最优.
；
上的一个映射，正整数数对
在映射f下的象为实数z，记作
. 对于任意的正整数
，映射
由下表给出：
__________，使不等式
成立的x的集合是_____________.
上选择一点C建造垃圾处理厂，其对市区的影响度与所选地 
的图像与函数
的图像所有交点的横坐标之和等于
是定义在R上的奇函数，若对于任意给定的不等实数
，不等式
恒成立，则不等式
的解集为( )
