题目内容
5.已知数列{an}的通项公式为an=n2cosnπ,Sn为它的前n项和,则$\frac{{S}_{2010}}{2011}$=1005.分析 通过an=n2cosnπ=$\left\{\begin{array}{l}{-{n}^{2},}&{n为奇数}\\{{n}^{2},}&{n为偶数}\end{array}\right.$,并项相加并利用平方差公式计算可知S2010=$\frac{2010×2011}{2}$,进而可得结论.
解答 解:依题意,an=n2cosnπ=$\left\{\begin{array}{l}{-{n}^{2},}&{n为奇数}\\{{n}^{2},}&{n为偶数}\end{array}\right.$,
∴S2010=-12+22-32+42-…-20092+20102
=(-12+22)+(-32+42)+…+(-20092+20102)
=(1+2)+(3+4)+…+(2009+2010)
=$\frac{2010×2011}{2}$,
∴$\frac{{S}_{2010}}{2011}$=$\frac{2010×2011}{2×2011}$=1005,
故答案为:1005.
点评 本题考查数列的通项及前n项和,考查运算求解能力,注意解题方法的积累,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.设函数f(x)=ex+g(x).若曲线y=g(x)在点P(0,g(0))处的切线方程是y=2x+1,则曲线y=f(x)在点Q(0,f(0))处的切线方程是( )
| A. | y=2x+1 | B. | y=2x+3 | C. | y=x+2 | D. | y=3x+2 |
14.由1,2,3,4组成没有重复数字的三位数,其中偶数的个数为( )
| A. | 6 | B. | 12 | C. | 24 | D. | 36 |
15.若函数f(x)=ex-ax2有三个不同零点,则a的取值范围是( )
| A. | ($\frac{e^2}{4}$,+∞) | B. | ($\frac{{{e^{\;}}}}{2}$,+∞) | C. | (1,$\frac{e^2}{4}$) | D. | (1,$\frac{{{e^{\;}}}}{2}$) |
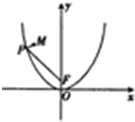 已知抛物线C:x2=2y的焦点为F,P为抛物线C上的任意一点,点M(-2,3),则|MP|+|PF|的最小值为$\frac{7}{2}$.
已知抛物线C:x2=2y的焦点为F,P为抛物线C上的任意一点,点M(-2,3),则|MP|+|PF|的最小值为$\frac{7}{2}$.