题目内容
如图,已知⊙A、⊙B都经过点C,BC是⊙A的切线,⊙B交AB于点D,连结CD并延长交⊙A于点E,连结AE.
(1)求证:AE⊥AB;
(2)求证:DE·DC=2AD·DB;
(3)如果DE·DC=8,AE=3,求BC的长.
思路解析:由圆中半径,可转化到两组角相等,抓住各角度之间的联系,易证∠DAE=90°,并证明△ADE∽△CDK.
(1)证明:
∵BC是⊙A的切线,
∴BC⊥AC,即∠ACB=90°.
∵BD=BC,AC=AE,
∴∠BDC=∠BCD,∠ACE=∠E.
∵∠BDC=∠ADE,
∴∠ADE=∠BCD.
∵∠ACD+∠BCD=90°,
∴∠ADE+∠E=90°.
∴∠DAE=90°,即AE⊥AB.
(2)证明:延长DB交⊙B于K点,连结CK,

∵DK是⊙B的直径,
∴∠DCK=90°.
∴∠EAD=∠KCD=90°.
∵∠ADE=∠CDK,
∴△ADE∽△CDK.∴![]() .
.
∴DE·DC=AD·DK.
∵DK=2BD,
∴DE·DC=2AD·BD.
(3)解:∵DE·DC=2AD·BD,DE·DC=8,∴2AD·DB=8.
∵AC2=AD·AK,
∴9=AD(AD+DK).
∴9=AD2+8.
∴AD=1.
∵2AD·DB=8,
∴BD=4.
∴BC=BD=4.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
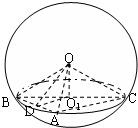 如图,已知A,B,C是表面积为48π的球面上的三点,AB=2,BC=4,∠ABC=60°,O为球心,则二面角O-AB-C的大小为:( )
如图,已知A,B,C是表面积为48π的球面上的三点,AB=2,BC=4,∠ABC=60°,O为球心,则二面角O-AB-C的大小为:( )A、
| ||||
B、
| ||||
C、arccos
| ||||
D、arccos
|
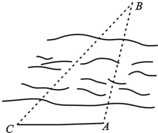 如图,已知A,B两点分别在河的两岸,某测量者在点A所在的河岸边另选定一点C,测得AC=50m,∠ACB=45°,∠CAB=105°,则A、B两点的距离为( )
如图,已知A,B两点分别在河的两岸,某测量者在点A所在的河岸边另选定一点C,测得AC=50m,∠ACB=45°,∠CAB=105°,则A、B两点的距离为( )A、50
| ||
B、25
| ||
C、25
| ||
D、50
|
 17、如图,已知A、B、C、D分别为过抛物线y2=4x焦点F的直线与该抛物线和圆(x-1)2+y2=1的交点,则|AB|•|CD|=
17、如图,已知A、B、C、D分别为过抛物线y2=4x焦点F的直线与该抛物线和圆(x-1)2+y2=1的交点,则|AB|•|CD|= 如图,已知A、B两点分别是椭圆C:
如图,已知A、B两点分别是椭圆C: (2012•江苏二模)如图,已知A、B是函数y=3sin(2x+θ)的图象与x轴两相邻交点,C是图象上A,B之间的最低点,则
(2012•江苏二模)如图,已知A、B是函数y=3sin(2x+θ)的图象与x轴两相邻交点,C是图象上A,B之间的最低点,则