Question

【题目】已知椭圆：上一点与两焦点构成的三角形的周长为,离心率为 .

（1）求椭圆的方程；

（2）设椭圆C的右顶点和上顶点分别为A、B，斜率为的直线l与椭圆C交于P、Q两点（点P在第一象限）.若四边形APBQ面积为，求直线l的方程.

Answer 1

【答案】（1）；（2）。

【解析】

（ 1）设椭圆的半焦距为c，由已知得，又，a2=b2+c2，联立解出即可得出；

（2）设直线方程为：代入椭圆并整理得：，利用韦达定理表示，分别计算Ａ，Ｂ到直线PQ的距离，即可表示四边形APBQ面积，从而得到直线l的方程.

（1）由题设得，又，

解得,

∴.

故椭圆的方程为.

（2）设直线方程为：代入椭圆并整理得：，

设，则.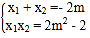

，

到直线PQ的距离为，

到直线PQ的距离为，

又因为在第一象限, 所以，

所以，

所以，

解得，

所以直线方程为．