题目内容
已知函数f(x)满足f(x+1)=-f(x),且x∈[0,2]时,f(x)=(x-1)2,则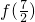 =
=
- A.

- B.
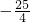
- C.

- D.

D
分析:根据已知中函数f(x)满足f(x+1)=-f(x),我们易判断函数f(x)为周期函数,且2为函数f(x)的一个周期,则根据x∈[0,2]时,f(x)=(x-1)2,我们易将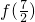 化为
化为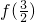 ,进而求出结果.
,进而求出结果.
解答:∵函数f(x)满足f(x+1)=-f(x),
∴f(x+2)=-f(x+1)=f(x),
∴2为函数f(x)的一个周期
∴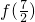 =
= =
=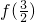
又∵当x∈[0,2]时,f(x)=(x-1)2,
∴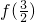 =(
=( -1)2=
-1)2=
故选D
点评:本题考查的知识点是函数的周期性,函数的值,其中根据已知中函数f(x)满足f(x+1)=-f(x),判断出2为函数f(x)的一个周期,是解答本题的关键.
分析:根据已知中函数f(x)满足f(x+1)=-f(x),我们易判断函数f(x)为周期函数,且2为函数f(x)的一个周期,则根据x∈[0,2]时,f(x)=(x-1)2,我们易将
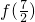 化为
化为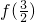 ,进而求出结果.
,进而求出结果.解答:∵函数f(x)满足f(x+1)=-f(x),
∴f(x+2)=-f(x+1)=f(x),
∴2为函数f(x)的一个周期
∴
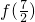 =
= =
=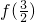
又∵当x∈[0,2]时,f(x)=(x-1)2,
∴
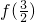 =(
=( -1)2=
-1)2=
故选D
点评:本题考查的知识点是函数的周期性,函数的值,其中根据已知中函数f(x)满足f(x+1)=-f(x),判断出2为函数f(x)的一个周期,是解答本题的关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目