题目内容
抛物线
上有两个定点
、
分别在对称轴的上下两侧，
为抛物线的焦点，并且|
|=2，|
|=5，在抛物线
这段曲线上求一点
，使
的面积最大，并求这个最大面积.
【答案】
解：由已知得
，不妨设点A在x轴上方且坐标为
，
由
得
所以A(1，2)，同理B(4,-4), 可得直线AB的方程为
.
设抛物线AOB这段曲线上任一点
，且
.
则点P到直线AB的距离
d=
所以当
时，d取最大值
，又
所以△PAB的面积最大值为
此时P点坐标为
【解析】略
练习册系列答案
口算小状元口算速算天天练系列答案
天天练口算系列答案
相关题目
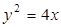上有两个定点A、B分别在对称轴的上、下两侧，F为抛物线的焦点，并且|FA|=2，|FB|=5，
上有两个定点A、B分别在对称轴的上、下两侧，F为抛物线的焦点，并且|FA|=2，|FB|=5，（1）求直线AB的方程。
上有两个定点
分别在对称轴的上、下两侧，
为抛物线的焦点，并且
。
的方程；
这段曲线上求一点
，使
的面积最大，并求最大面积.（其中
为坐标原点）