题目内容
若正方体ABCD-A1B1C1D1的外接球O的体积为4
π，则球心O到正方体的一个面ABCD的距离为（ ）
| 3 |
| A、1 | B、2 | C、3 | D、4 |
分析：根据球的体积公式算出球的半径R=
，从而得到正方体的对角线长为2
，可得正方体的棱长为2．再由球心O是正方体ABCD-A1B1C1D1的中心，得到点O到正方体的一个面的距离等于正方体棱长的一半，从而算出答案．
| 3 |
| 3 |
解答：解：
设球O的半径为R，正方体ABCD-A1B1C1D1的棱长为a，
∵正方体ABCD-A1B1C1D1内接于球O，
∴正方体的对角线长等于球O的直径，可得2R=
a．
又∵球O的体积为4
π，
∴V=
•R3=4
π，解得R=
，
由此可得
a=2R=2
，解得a=2．
∵球O是正方体ABCD-A1B1C1D1的外接球，
∴点O是正方体ABCD-A1B1C1D1的中心，
可得点O到正方体的一个面的距离等于正方体棱长的一半，即d=
a=1．
因此，球心O到正方体的一个面ABCD的距离等于1．
故选：A
设球O的半径为R，正方体ABCD-A1B1C1D1的棱长为a，∵正方体ABCD-A1B1C1D1内接于球O，
∴正方体的对角线长等于球O的直径，可得2R=
| 3 |
又∵球O的体积为4
| 3 |
∴V=
| 4π |
| 3 |
| 3 |
| 3 |
由此可得
| 3 |
| 3 |
∵球O是正方体ABCD-A1B1C1D1的外接球，
∴点O是正方体ABCD-A1B1C1D1的中心，
可得点O到正方体的一个面的距离等于正方体棱长的一半，即d=
| 1 |
| 2 |
因此，球心O到正方体的一个面ABCD的距离等于1．
故选：A
点评：本题给出正方体的外接球的体积，求球心到正方体一个面的距离．着重考查了正方体的性质、球的体积公式与球内接多面体等知识，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
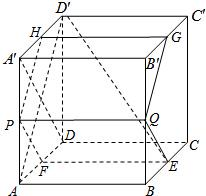如图，在棱长为1的正方体ABCD-A′B′C′D′中，AP=BQ=b（0＜b＜1），截面PQEF∥A′D，截面PQGH∥AD′．
（2012•海淀区一模）在棱长为1的正方体ABCD-A′B′C′D′中，若点P是棱上一点，则满足|PA|+|PC′|=2的点P的个数为（ ）
如图，在正方体ABCD-A′B′C′D′中，E，F分别是AB′，BC′的中点．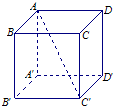 
（2012•海淀区一模）在正方体ABCD-A'B'C'D'中，若点P（异于点B）是棱上一点，则满足BP与AC'所成的角为45°的点P的个数为（ ）