题目内容
正四棱锥S-ABCD底面边长为2,高为1,E是边BC的中点,动点P在四棱锥表面上运动,并且总保持 ,则动点P的轨迹的周长为
,则动点P的轨迹的周长为
- A.

- B.
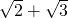
- C.

- D.

B
分析:根据题意可知点P的轨迹为三角形EFG,其中G、F为中点,根据中位线定理求出EF、GE、GF,从而求出轨迹的周长.
解答: 解:由题意知:点P的轨迹为如图所示的三角形EFG,其中G、F为中点,
解:由题意知:点P的轨迹为如图所示的三角形EFG,其中G、F为中点,
∴EF=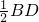 =
= ,
,
∵SB= =
=
∴GE=GF= =
=
∴轨迹的周长为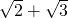
故选B.
点评:本题主要考查了轨迹问题,以及点到面的距离等有关知识,同时考查了空间想象能力,计算推理能力,属于中档题.
分析:根据题意可知点P的轨迹为三角形EFG,其中G、F为中点,根据中位线定理求出EF、GE、GF,从而求出轨迹的周长.
解答:
 解:由题意知:点P的轨迹为如图所示的三角形EFG,其中G、F为中点,
解:由题意知:点P的轨迹为如图所示的三角形EFG,其中G、F为中点,∴EF=
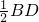 =
= ,
,∵SB=
 =
=
∴GE=GF=
 =
=
∴轨迹的周长为
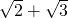
故选B.
点评:本题主要考查了轨迹问题,以及点到面的距离等有关知识,同时考查了空间想象能力,计算推理能力,属于中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 如图,正四棱锥S-ABCD中,E是侧棱SC的中点,异面直线SA和BC所成角的大小是60°.
如图,正四棱锥S-ABCD中,E是侧棱SC的中点,异面直线SA和BC所成角的大小是60°. 12、如图在正四棱锥S-ABCD中,E是BC的中点,P点在侧面△SCD内及其边界上运动,并且总是保持PE⊥AC,则动点P的轨迹与△SCD组成的相关图形是( )
12、如图在正四棱锥S-ABCD中,E是BC的中点,P点在侧面△SCD内及其边界上运动,并且总是保持PE⊥AC,则动点P的轨迹与△SCD组成的相关图形是( )