Question

12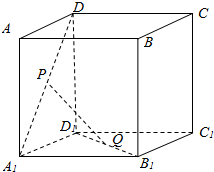．如图，正方体的棱长为a，P、Q分别为A₁D、B₁D₁的中点
（1）求证：PQ∥平面D₁C₁CD
（2）求PQ的长．

Answer 1

分析 （1）连结AD₁，AB₁，由三角形中位线定理和正方体结构特征推导出PQ∥DC₁，由此能证明PQ∥平面D₁C₁CD．
（2）P、Q分别为A₁D、B₁D₁的中点，利用三角形中位线定理能求出PQ的长．

解答 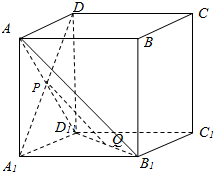（1）证明：连结AD₁，AB₁，
∵正方体的棱长为a，P、Q分别为A₁D、B₁D₁的中点，
∴P，Q分别是AD₁，D₁B的中点，
∴PQ∥AB₁，∵AB₁∥DC₁，∴PQ∥DC₁，
∵PQ?平面D₁C₁CD，DC₁?平面D₁C₁CD，
∴PQ∥平面D₁C₁CD．
（2）解：∵P、Q分别为A₁D、B₁D₁的中点，
∴PQ=$\frac{1}{2}$AB₁=$\frac{1}{2}$$\sqrt{{a}^{2}+{a}^{2}}$=$\frac{\sqrt{2}}{2}a$．

点评 本题考查线面平行的证明，考查线段长的求法，是基础题，解题时要认真审题，注意空间思维能力的培养．