已知圆x2+y2=4上存在两点到点的距离为1.则实数m的取值范围为$\frac{\sqrt{2}}{2}$＜a＜$\frac{3\sqrt{2}}{2}$．题目和参考答案——青夏教育精英家教网—

题目内容

1．已知圆x²+y²=4上存在两点到点（m，m）（m＞0）的距离为1，则实数m的取值范围为$\frac{\sqrt{2}}{2}$＜a＜$\frac{3\sqrt{2}}{2}$．

分析由题意得，点（m，m）到圆心（0，0）的距离大于1小于3，解一元二次不等式组求得m的取值范围．

解答解：由题意得，点（m，m）到圆心（0，0）的距离大于1小于3，
即 1＜$\sqrt{{m}^{2}+{m}^{2}}$＜3，∴$\frac{\sqrt{2}}{2}$＜a＜$\frac{3\sqrt{2}}{2}$，
故答案为：$\frac{\sqrt{2}}{2}$＜a＜$\frac{3\sqrt{2}}{2}$．

点评本题考查点与圆的位置关系，两点间的距离公式的应用，一元二次不等式的解法，判断点（m，m）到圆心（0，0）的距离大于1小于3是解题的关键．

练习册系列答案

相关题目

11．

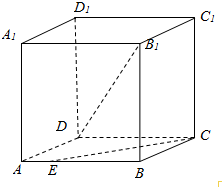如图，正方体ABCD-A₁B₁C₁D₁的棱长为1，点E在棱AB上，且AE=m．已知异面直线DB₁与CE所成角的余弦值等于$\frac{{\sqrt{3}}}{15}$，求m的值．

12．

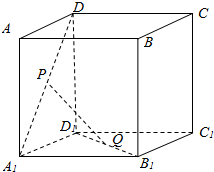如图，正方体的棱长为a，P、Q分别为A₁D、B₁D₁的中点
（1）求证：PQ∥平面D₁C₁CD
（2）求PQ的长．

9．设f（x）是定义在（0，+∞）上的增函数，且对任意x，y∈（0，+∞），都有f（xy）=f（x）+f（y）．
若f（3）=1，f（a）＞f（a-1）+2，则a的取值范围（1，$\frac{9}{8}$）．

16．“x＞3”是“x≥2”的充分不必要条件，（从“充分不必要”，“必要不充分”，“充要”或“既不充分又不必要”选一个填空）

6．如图1，一座抛物线型拱桥，水面离拱顶8m，水面宽16m，如图2，一艘船的宽度为12m，船的甲板与水面距离为1m，船上两根高为a m的杆垂直于船的甲板，且到甲板左右两边的距离为2m，现船正面正对桥洞（船截面的中轴线与抛物线对称轴重合时）通过该拱桥
（1）当a=3时，该渔船是否能安全通过该拱桥？
（2）若该渔船能安全通过该拱桥，求a的最大值．

13．已知1＜x＜10，令a=lgx，b=log₂（lgx），c=2^lgx，则a，b，c的大小关系是（　　）

10．在△ABC中，角A，B，C的对边分别为a，b，c，cos²$\frac{A}{2}$=$\frac{b+c}{2c}$，则△ABC的形状一定是（　　）

11．已知函数$f（x）=A（sin\frac{x}{2}cosφ+cos\frac{x}{2}sinφ）（A＞0，0＜φ＜\frac{π}{2}）$的最大值是2，且f（0）=1．
（Ⅰ）求φ的值；
（Ⅱ）已知锐角△ABC的内角A，B，C的对边分别为a，b，c，若a=2，f（2A）=$\sqrt{3}$，2bsinC=$\sqrt{2}$c．求△ABC的面积．

试题分类