题目内容
3.已知曲线C是与两个定点A(1,0),B(4,0)的距离比为$\frac{1}{2}$的动点的轨迹(1)求曲线C的方程;
(2)求曲线C上的动点到直线l:x-y+3=0的距离的最大值.
分析 (1)由题意,设此曲线上的任意一点P(x,y),则|AP|=$\sqrt{(x-1)^{2}+{y}^{2}}$,|BP|=$\sqrt{(x-4)^{2}+{y}^{2}}$,$\frac{|AP|}{|BP|}=\frac{1}{2}$,代入化简即可;
(2)由题意画出图形,数形结合得答案.
解答 解:(1)设此曲线上的任意一点P(x,y),则|AP|=$\sqrt{(x-1)^{2}+{y}^{2}}$,|BP|=$\sqrt{(x-4)^{2}+{y}^{2}}$,
由题意可得,$\frac{|AP|}{|BP|}=\frac{1}{2}$,
则$\sqrt{(x-4)^{2}+{y}^{2}}$=2$\sqrt{(x-1)^{2}+{y}^{2}}$,整理得x2+y2=4,
∴所求曲线C的方程为x2+y2=4;
(2)如图, 圆心O到直线x-y+3=0的距离|OA|=$\frac{|3|}{\sqrt{2}}=\frac{3\sqrt{2}}{2}$,
圆心O到直线x-y+3=0的距离|OA|=$\frac{|3|}{\sqrt{2}}=\frac{3\sqrt{2}}{2}$,
∴曲线C上的动点到直线l:x-y+3=0的距离的最大值为$\frac{3\sqrt{2}}{2}+2$.
点评 本题考查了轨迹方程的求法,训练了点到直线的距离公式的应用,考查了数形结合的解题思想方法,属于中档题.

练习册系列答案
相关题目
13.已知1<x<10,令a=lgx,b=log2(lgx),c=2lgx,则a,b,c的大小关系是( )
| A. | a<b<c | B. | b<a<c | C. | c<a<b | D. | b<c<a |
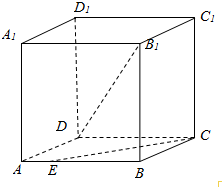 如图,正方体ABCD-A1B1C1D1的棱长为1,点E在棱AB上,且AE=m.已知异面直线DB1与CE所成角的余弦值等于$\frac{{\sqrt{3}}}{15}$,求m的值.
如图,正方体ABCD-A1B1C1D1的棱长为1,点E在棱AB上,且AE=m.已知异面直线DB1与CE所成角的余弦值等于$\frac{{\sqrt{3}}}{15}$,求m的值.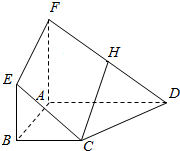 如图,四边形ABEF与四边形ABCD都是梯形,BC∥AD,BC=$\frac{1}{2}$AD,BE∥AF,BE=$\frac{1}{2}$AF,H是FD的中点.
如图,四边形ABEF与四边形ABCD都是梯形,BC∥AD,BC=$\frac{1}{2}$AD,BE∥AF,BE=$\frac{1}{2}$AF,H是FD的中点.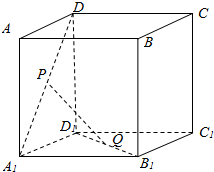 如图,正方体的棱长为a,P、Q分别为A1D、B1D1的中点
如图,正方体的棱长为a,P、Q分别为A1D、B1D1的中点