题目内容
已知集合A={(a,c)|0<a<2,0<c<2,a,c∈R},则任取(a,c)∈A,关于x的方程ax2+2x+c=0无实根的概率( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:若关于x的方程ax2+2x+c=0有实根,则ac≤1,以c横轴,a为纵轴,作出平面直角坐标系,令a=2,得c=
,利用微积分求出关于x的方程ax2+2x+c=0有实根的概率,由此利用对立事件概率计算公式能求出关于x的方程ax2+2x+c=0无实根的概率.
| 1 |
| 2 |
解答:
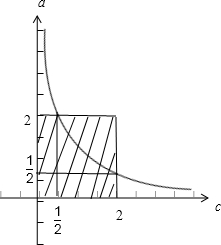 解:若关于x的方程ax2+2x+c=0有实根,
解:若关于x的方程ax2+2x+c=0有实根,
则△=4-4ac≥0,得ac≤1,
以c横轴,a为纵轴,作出平面直角坐标系,
令a=2,得c=
,
则关于x的方程ax2+2x+c=0有实根的概率为:
p=
=
(1+ln2-ln
)
=
,
∴关于x的方程ax2+2x+c=0无实根的概率为:
p1=1-
=
.
故选:D.
 解:若关于x的方程ax2+2x+c=0有实根,
解:若关于x的方程ax2+2x+c=0有实根,则△=4-4ac≥0,得ac≤1,
以c横轴,a为纵轴,作出平面直角坐标系,
令a=2,得c=
| 1 |
| 2 |
则关于x的方程ax2+2x+c=0有实根的概率为:
p=
2×
| ||||||||
| 2×2 |
=
| 1 |
| 4 |
| 1 |
| 2 |
=
| 1+2ln2 |
| 4 |
∴关于x的方程ax2+2x+c=0无实根的概率为:
p1=1-
| 1+2ln2 |
| 4 |
| 3-2ln2 |
| 4 |
故选:D.
点评:本题考查几何概率概率的求法,是中档题,解题时要注意微积分的合理运用.

练习册系列答案
相关题目
下列关于函数f(x)=2sin(2x+
)的结论,其中正确结论是( )
①图象关于原点成中心对称;
②图象关于直线x=
成轴对称;
③图象可由函数y=2sin2x的图象向左平移
个单位得到;
④图象向左平移
个单位,即得到函数y=2cos2x的图象.
| π |
| 3 |
①图象关于原点成中心对称;
②图象关于直线x=
| π |
| 12 |
③图象可由函数y=2sin2x的图象向左平移
| π |
| 3 |
④图象向左平移
| π |
| 12 |
| A、①② | B、②③ | C、③④ | D、②④ |
从2件一等品和2件二等品中任取两件,是对立事件的是( )
| A、至少有1件二等品,全是二等品 |
| B、至少有1件二等品,至少有1件一等品 |
| C、恰有1件二等品,恰有2件二等品 |
| D、至少有1件二等品,全是一等品 |
读如图程序框图,若输入的a,b,c的值分别为1,2,3,则输出的结果是( )

| A、1 | B、2 | C、3 | D、c |
若二项式(2x+
)8的展开式中的常数项为70,则实数a可以为( )
| a |
| x |
| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
设i为虚数单位,则复数
的虚部是( )
| 1+2i |
| i |
| A、1 | B、i | C、-1 | D、-i |
一只不透明的布袋中有三种小球(除颜色以外没有任何区别),分别是2个红球,3个白球和5个黑球,每次只摸出一只小球,观察后均放回搅匀.在连续9次摸出的都是黑球的情况下,第10次摸出红球的概率是( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、以上都不对 |
 如图,单位正方形ABCD,在正方形内(包括边界)任取一点M,求:
如图,单位正方形ABCD,在正方形内(包括边界)任取一点M,求: